Question

In the figure below, the switches ${{S}_{1}}$ and ${{S}_{2}}$ are closed simultaneously at t=0 and a current starts to flow in the circuit. Both the batteries have the same magnitude of the electromotive force (emf) and the polarities are as indicated in the figure. Ignore mutual inductance between the inductors. The current I in the middle wire reaches its maximum magnitude ${{I}_{\max }}$ at time $t=\tau $. Which of the following statements is/are true?

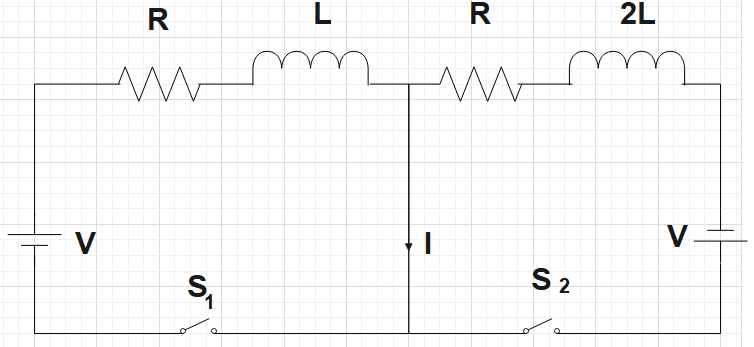
A. ${{I}_{\max }}=\dfrac{V}{2R}$
B. ${{I}_{\max }}=\dfrac{V}{4R}$
C. $\tau =\dfrac{L}{R}\ln 2$
D. $\tau =\dfrac{2L}{R}\ln 2$

Answer 1

Hint: As a very first step, one could mark the directions of current in the two loops of the circuit. Then you could find the expression for maximum current accordingly. We could say that for its maximum value, its time derivative is zero. Hence get the required quantities accordingly.

Complete answer:
As a first step, one could mark the direction of the current flow in both the loops of the given circuit. We are already given that the middle wire reaches a certain maximum current ${{i}_{\max }}$ at a certain time $\tau $.

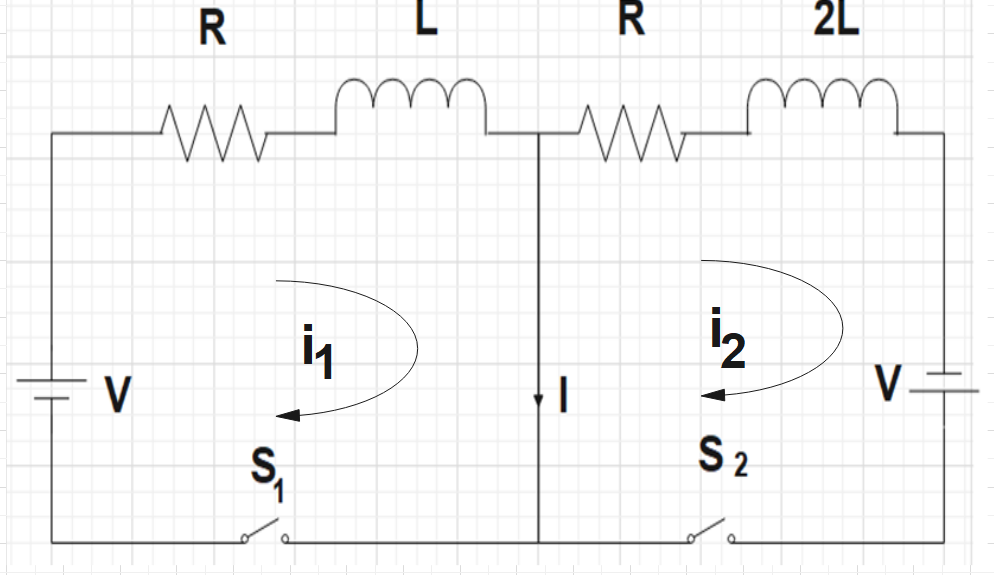
This maximum current would be,
${{i}_{\max }}={{i}_{1}}-{{i}_{2}}$
Also,
$\Delta i={{i}_{2}}-{{i}_{1}}=\dfrac{V}{R}\left( 1-{{e}^{-\left( \dfrac{R}{2L} \right)t}} \right)-\dfrac{V}{R}\left( 1-{{e}^{\left( \dfrac{R}{2L} \right)t}} \right)$
For the maximum current we have, $\dfrac{di}{dt}=0$
$\Rightarrow \dfrac{V}{R}\left( -\dfrac{R}{L}{{e}^{-\dfrac{R}{L}t}}-\left( -\dfrac{R}{2L} \right){{e}^{-\dfrac{R}{2L}t}} \right)=0$
$\Rightarrow {{e}^{-\left( \dfrac{Rt}{L} \right)}}=\dfrac{1}{2}{{e}^{-\left( \dfrac{Rt}{2L} \right)}}$
$\Rightarrow \dfrac{R}{2L}t=\ln 2$
So, for maximum current we have the time as,
$t=\dfrac{2L}{R}\ln 2$
Substituting this t in expression for maximum current we get,
${{i}_{\max }}=\dfrac{V}{R}\left( {{e}^{\dfrac{R}{L}\left( \dfrac{2L}{R}\ln 2 \right)}}-{{e}^{-\dfrac{R}{2L}\left( \dfrac{2L}{R}\ln 2 \right)}} \right)$
$\therefore \left| {{I}_{\max }} \right|=\dfrac{V}{R}\left( \dfrac{1}{4}-\dfrac{1}{2} \right)=\dfrac{V}{4R}$
Therefore, we found the time at which the current becomes maximum to be, $t=\dfrac{2L}{R}\ln 2$and the maximum current to be ${{I}_{\max }}=\dfrac{V}{4R}$.

Hence, options B and D are true.

Note:
Since we have an inductor and resistor connected in series in the given circuit, we have found the current accordingly in two loops present in the given circuit. You may be worried about the mutual inductance present due to the two inductors but we are clearly asked to ignore the same.