Question

In the figure below ABCD is a parallelogram. AF and EC are the bisectors of \[\angle DAB\] and \[\angle BAC\] respectively, then \[AF\parallel CE\]

(a) True
(b) False

Answer 1

Hint: We solve this problem by using the bisector of an angle and the parallel lines theorems. The angular bisector is a line segment that divides the angle into two equal parts. We use some the conditions of parallelogram and parallel lines to solve this problem.
(1) For a parallelogram the opposite angles are equal.
(2) For a set of two parallel lines the transversal divides the parallel lines at equal corresponding angle and vice versa. That is for the following parallel lines we have

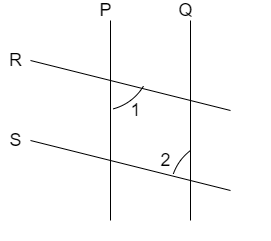
Here, if \[P\parallel Q,R\parallel S\] then the angle 1 and angle 2 both are equal and vice versa.

Complete step by step answer:
We are given that ABCD is a parallelogram.
We know that the opposite angles of a parallelogram are equal to each other.
By using the above condition to given parallelogram we get
\[\Rightarrow \angle DCB=\angle DAB........equation(i)\]
We are given that the lines AF and EC are the bisectors of \[\angle DAB\] and \[\angle BAC\] respectively
We know that the bisector of an angle divides the angle into two equal parts.
By using the above condition to both the angles \[\angle DAB\] and \[\angle BAC\] we get
\[\Rightarrow \angle DAF=\angle FAE\]
\[\Rightarrow \angle DCE=\angle ECB\]
Now, let us take the equation (i) and divide the two angles as the sum of other two angles that are divided then we get
\[\Rightarrow \angle DCE+\angle ECB=\angle DAF+\angle FAE\]
Now by substituting the above equal angles then we get
\[\begin{align}
  & \Rightarrow 2\angle DCE=2\angle FAE \\
 & \Rightarrow \angle DCE=\angle FAE \\
\end{align}\]
We know that for a set of two parallel lines the transversal divides the parallel lines at equal corresponding angle and vice versa. That is for the following parallel lines we have

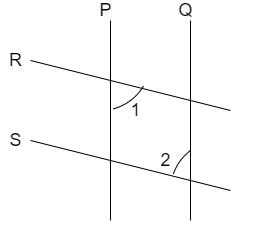
Here, if \[P\parallel Q,R\parallel S\] then the angle 1 and angle 2 both are equal and vice versa.
Here, we know that vice versa means if one happens then another will happen.
Here we can see that \[\angle DCE=\angle FAE\] from the figure.
So, from the above condition we can say that \[FC\parallel AE\] and \[AF\parallel CE\]
Therefore, we can conclude that the quadrilateral AECF is a parallelogram and \[AF\parallel CE\]

So, the correct answer is “Option a”.

Note: We can have the other explanation of the above problem.
We have the given figure as

We have a standard result of a parallelogram that is the angular bisectors of the opposite angles of a parallelogram are always parallel.
Here we are given that AF and EC are the bisectors of \[\angle DAB\] and \[\angle BAC\]
Here, we can see that \[\angle DAB\] and \[\angle BAC\] are opposite angles of the parallelogram ABCD.
So, by using the standard result that is mentioned above we can say that \[AF\parallel CE\]
Therefore option (a) is the correct answer.