Question

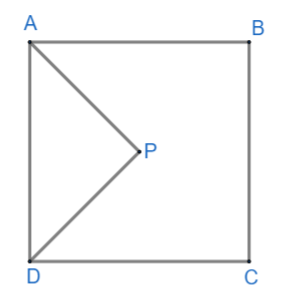
In the figure, AP and DP are bisectors of $\angle D$ Prove that \[2\angle APD=\angle B+\angle C\]

Answer 1

Hint: As AP and DP are angle bisectors they must be cutting angle $\angle A\text{ and }\angle \text{D}$ respectively in two equal angles. Make an equation using the sum of interior angles of a quadrilateral ABCD and an equation using interior angles of a triangle formed by bisectors $\Delta APD$. Subtracting these two equations would lead to the results.

Complete step by step answer:
In the given figure, AP and DP are bisectors of two adjacent angles A and D of given quadrilateral ABCD.
Bisector divides any given entity in two equal parts. Given AP and DP are angle bisector which are bisecting angles $\angle A\text{ and }\angle \text{D}$ respectively into two equal half angles. We need to prove that,
\[2\angle APD=\angle B+\angle C\]

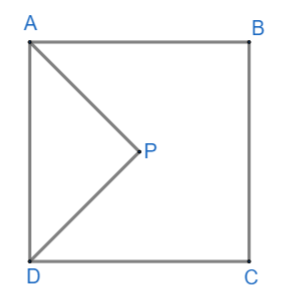
The given figure is a quadrilateral. A quadrilateral is a close geometry which has 4 sides. The sum of all the angles (interior) of a quadrilateral $\Rightarrow {{360}^{\circ }}$
All the interior angles are \[\angle A,\angle B,\angle C,\angle D\]
\[\Rightarrow \angle A+\angle B+\angle C+\angle D={{360}^{\circ }}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (1)}\]
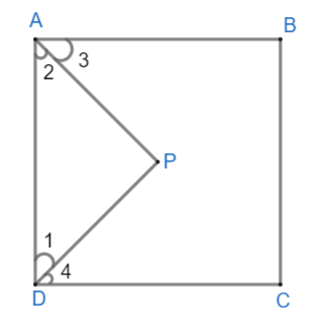
In the figure, AP is bisecting angle A. Therefore, $\angle 2=\angle 3$ similarly DP bisects angle D. Therefore, $\angle 1=\angle 4$

Now from equation (1),
\[\Rightarrow \angle A+\angle B+\angle C+\angle D={{360}^{\circ }}\]
Multiplying both sides with $\dfrac{1}{2}$
\[\begin{align}
  & \Rightarrow \dfrac{1}{2}\times \left( \angle A+\angle B+\angle C+\angle D \right)=\dfrac{1}{2}\times {{360}^{\circ }} \\
 & \Rightarrow \dfrac{1}{2}\angle A+\dfrac{1}{2}\angle B+\dfrac{1}{2}\angle C+\dfrac{1}{2}\angle D={{180}^{\circ }}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (2)} \\
\end{align}\]
Observe triangle $\angle \text{APD}$ which is being formed from the bisectors AP and DP.
The sum of all interior angles of triangle is ${{180}^{\circ }}$
Therefore, \[\angle 1+\angle 2+\angle APD={{180}^{\circ }}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (3)}\]
Since, \[\begin{align}
  & \angle 1=\dfrac{1}{2}\angle D\text{ (as DP is angle bisector)} \\
 & \angle \text{2=}\dfrac{1}{2}\angle A\text{ (as AP is angle bisector)} \\
\end{align}\]
So, our equation (3) becomes,
\[\dfrac{1}{2}\angle D+\dfrac{1}{2}\angle A+\angle APD={{180}^{\circ }}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (4)}\]
Now, subtracting equation (2) from equation (4) we get:
\[\begin{align}
  & -\dfrac{1}{2}\angle B-\dfrac{1}{2}\angle C+\angle APD=0 \\
 & -\dfrac{1}{2}\left( \angle B+\angle C \right)=-\angle APD \\
 & \angle B+\angle C=2\angle APD \\
 & \Rightarrow 2\angle APD=\angle B+\angle C \\
\end{align}\]
Hence, proved.

Note: Here in the given question, students might wrongly assume the given figure as a square or a rectangle, such misconception can lead to wrong results. Solve the problem with basic knowledge of angle bisectors and sum of interior angles of some polygons. In the above solution, we can also multiply equation 4 with 2 to obtain $\angle D+\angle A+2\angle APD={{360}^{\circ }}$ and then subtract equation 1 from this. Both ways we will get the same answer.