Question

In the figure, $ \angle X = 62^\circ $ , $ \angle XYZ = 54^\circ $ . If $ YO $ and $ ZO $ are the bisectors of $ \angle XYZ $ and $ \angle XZY $ respectively of $ \Delta XZY $ , find $ \angle OZY $ and $ \angle YOZ. $

Answer 1

Hint: Use the property that the sum of angles of a triangle is equal to $ {180^0} $ to first find $ \angle XZY $ . Then use the property of angle bisectors to find $ \angle OZY $ . Then use this angle and the angle sum property of a triangle to find $ \angle YOZ $

Complete step-by-step answer:

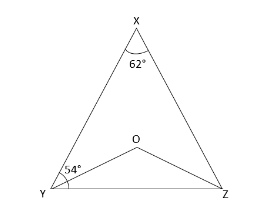
It is given in the question that,
 $ \angle X = 62^\circ $ , $ \angle XYZ = 54^\circ $
And YO and ZO are angle bisectors of $ \angle XYZ $ and $ \angle XZY $
We know that the addition of all three angles of a triangle is equal to $ 180^\circ $
i.e. $ \angle XYZ + \angle YXZ + \angle XZY = 180^\circ $
by substituting the given values in the above equation, we can write.
 $ {54^0} + {62^0} + \angle XZY = 180^\circ $
By simplifying it, we get
 $ \therefore \angle XZY = 180^\circ - 116^\circ $
 $ \Rightarrow \angle XZY = 64^\circ $
Now, since, OY is an angle bisector. We can write,
 $ \angle OYZ = \dfrac{1}{2} \times 54 $
 $ \Rightarrow \angle OYZ = 27^\circ $
Similarly, since, OZ is angle bisector, we can write,
 $ \angle OZY = \dfrac{1}{2} \times 64 $
 $ \Rightarrow \angle OZY = 32^\circ $
So, now, in $ \Delta OYZ $
We know that the sum of the angles of a triangle is equal to \[{180^0}\]. Therefore, we can write,
 $ \angle YOZ + \angle OYZ + \angle OZY = 180^\circ $
By substituting the values of $ \angle OYZ $ and $ \angle OZY $ , we get
 $ \angle YOZ + 27^\circ + 32^\circ = 180^\circ $
By simplifying it, we get
 $ \angle YOZ = 121^\circ $
Therefore, form the above explanation, we can conclude that, $ \angle OZY = 32^\circ $ and $ \angle YOZ = 121^\circ $

Note: You might be tempted to think that OY and OZ are equal. And hence, you might use the property of isosceles triangles. But that would be incorrect. OY and OZ can only be equal if the $ \Delta XYZ $ is either isosceles or equilateral triangle. Which is not given in the question. So you cannot assume that.