Question

In the figure, $\angle P + \angle Q + \angle R + \angle S + \angle T = 2$ Right angles.
A) True
B) False

Answer 1

Hint:
Angle of straight line is ${180^\circ }$ and Sum of measure of interior angles is $(n - 2) \times {180^\circ }$. By using these both we will prove the given expression for the figure.

Complete step by step solution:

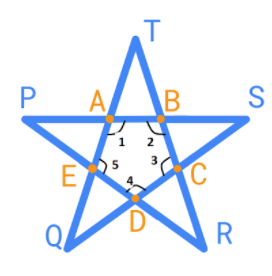
We know that a straight line have angle${180^\circ }$,
Therefore, $\angle PAE + \angle 1 = {180^\circ } \Rightarrow \angle PAE = {180^\circ } - \angle 1$
Similarly, $\angle PEA + \angle 5 = {180^\circ } \Rightarrow \angle PEA = {180^\circ } - \angle 5$
In $\vartriangle PAE$ , $\angle PAE + \angle PEA + \angle APE = {180^\circ }$ (Sum of angles of triangle.)
$ \Rightarrow \angle APE = \angle 1 + \angle 5 - {180^\circ } = \angle P$
Similarly,
$\angle BSC = \angle 2 + \angle 3 - {180^\circ } = \angle S$
$\angle DRC = \angle 3 + \angle 4 - {180^\circ } = \angle R$
$\angle DQE = \angle 4 + \angle 5 - {180^\circ } = \angle Q$
$\angle ATS = \angle 1 + \angle 2 - {180^\circ } = \angle T$
Now adding all above equation:
$ \Rightarrow \angle P + \angle Q + \angle R + \angle S + \angle T = 2(\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5) - ({180^\circ } \times 5)$- (A)
Now, from figure ABCDE is a polygon having 5 sides called pentagon. Therefore, Sum of interior angles of polygon $ = (n - 2) \times {180^\circ }$ where n = 5.
Therefore, $\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 = (5 - 2) \times {180^\circ } = 3 \times {180^\circ } = 540$
Therefore equation (A) becomes,
$ \Rightarrow \angle P + \angle Q + \angle R + \angle S + \angle T = 2 \times 540 - 900$
$ \Rightarrow \angle P + \angle Q + \angle R + \angle S + \angle T = 1080 - 900 = 180 = 2 \times $Right angle [Right angle =${90^\circ }$]

Hence, Option (A) is correct.

Note:
While solving first you have to know the sum of interior angles of basic structure for example triangles have sum of angles 180 degree, for quadrilateral sum of interior angles is 360 degree.
Also, do not confuse yourself in $\angle ABC$ or $\angle B$ written because both are the same. The prefix or name or vertex point in the centre of angle full name is the angle. For example- $\angle ABC{\text{ and }}\angle B$ are the same.
Additional Information:
Polygon- In Geometry, polygon is a plane figure that is described by a finite number if straight-line segments connected to form a closed figure
Sum of interior angles of any polygon$ = (n - 2) \times {180^\circ }$, where n is the sides of a polygon.
Sum of exterior angles of any polygon $ = {360^\circ }$
There are polygons which have names according to the sides:
1 Side = monogon
2 sides = digon
3 sides = triangle or trigon
4 sides = quadrilateral or tetragon
5 sides = pentagon
6 sides = hexagon
7 sides = heptagon or septagon
8 sides = octagon
9 sides = nonagon or enneagon
10 sides = decagon and so on.