Question

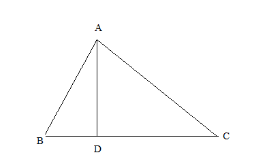
In the figure, $ \angle B $ of $ \Delta ABC $ is an acute angle and $ AD \bot BC $ , prove that $ A{C^2} = A{B^2} + B{C^2} - 2 \times BC \times BD $ .

Answer 1

Hint: Use the Pythagoras theorem in both the triangles $ ABD $ and $ ACD $ . Find the relationship of sides $ BD $ , $ DC $ and $ BC $ . Use the result to get the expression to be proved.

Complete step-by-step answer:
As per given that $ AD \bot BC $ , use the Pythagoras theorem in $ \Delta ABD $ .
 $
  {P^2} + {B^2} = {H^2} \\
  A{D^2} + B{D^2} = A{B^2} \\
  A{D^2} = A{B^2} - B{D^2}\;\;\;\;\; \ldots \left( 1 \right) \;
  $
 As per given that $ AD \bot BC $ , use the Pythagoras theorem in $ \Delta ACD $ .
 $
  {P^2} + {B^2} = {H^2} \\
  A{D^2} + C{D^2} = A{C^2}\;\;\;\; \ldots \left( 2 \right) \;
  $
Substitute the value of $ A{D^2} $ from equation $ \left( 1 \right) $ in equation $ \left( 2 \right) $ :
 $
  A{D^2} + C{D^2} = A{C^2} \\
  A{C^2} = \left( {A{B^2} - B{D^2}} \right) + C{D^2}\;\;\;\;\;\; \ldots \left( 3 \right) \;
  $
According to the diagram it is obvious that $ CD = BC - DB $ . Substitute the value $ CD $ in equation $ \left( 3 \right) $ .
 $
  A{C^2} = \left( {A{B^2} - B{D^2}} \right) + C{D^2} \\
   = \left( {A{B^2} - B{D^2}} \right) + {\left( {BC - BD} \right)^2} \\
   = \left( {A{B^2} - B{D^2}} \right) + \left( {B{C^2} + B{D^2} - 2 \times BC \times BD} \right) \\
   = A{B^2} + B{C^2} - 2 \times BC \times BD \;
  $
Hence, the result $ A{C^2} = A{B^2} + B{C^2} - 2 \times BC \times BD $ is true.
So, the correct answer is “ $ A{C^2} = A{B^2} + B{C^2} - 2 \times BC \times BD $ ”.

Note: As both the triangles are given to be right angled triangles as one of the angles is the right angle. So, we can use the Pythagoras theorem in both the triangles as it is used only for right angled triangles. The Pythagoras theorem states the relationship between the hypotenuse, base and perpendicular lengths of the triangle which is given as $ {P^2} + {B^2} = {H^2} $ i.e. the sum of the squares of two sides of triangle is equal to the square of third side of the triangle.