Question

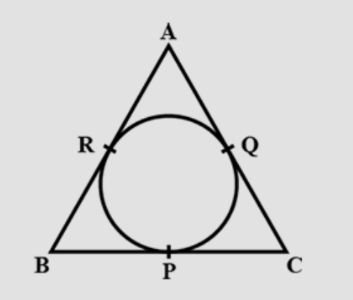
In the figure, an isosceles triangle ABC, with AB=AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.

Answer 1

Hint: We have to use the tangents concept to solve the given problem. Tangent segments drawn from an external point to a circle are congruent.

Given an isosceles triangle ABC with AB=AC, circumscribing a circle.
We need to prove P bisects BC.
Proof: AR and AQ are the tangents drawn from an external point A to the circle.
Therefore, AR=AQ (Tangents drawn from an external point to the circle are equal)
Similarly, BR=BP and CP=CQ.
It is given that in triangle ABC, AB=AC.
$$ \Rightarrow $$ AR+RB=AQ+QC
$$ \Rightarrow $$ BR=QC (As AR=AQ)
$$ \Rightarrow $$ BP=CP (as BR=BP and CP=CQ)
$$ \Rightarrow $$ P bisects BC.
Hence proved.

Note: Here we used the property that the tangents drawn from an external point to the circle are congruent. It is because that a tangent at any point of a circle is perpendicular to the radius through the point of contact.