Question

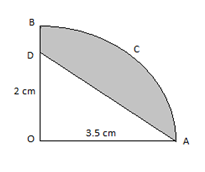
In the figure alongside, OAB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded portion. Take \[\pi ={}^{22}/{}_{7}.\]

Answer 1

Hint:- The area of the shaded region can be obtained by subtracting the area of triangle AOD from the area of the quarter of the circle, by doing so you will get the area of the shaded region.

Complete step-by-step solution -
From the figure we can say that OACB is a quarter of a circle. What we need to do is find the area of the shaded region in the figure.
We have been given the length of OA = 3.5 cm and OD = 2 cm.
We can say that OD is also the radius of the quarter of the circle. We can take the radius of the quarter as ‘r’.
\[\therefore OA=r=3.5cm.\]
We know the area of the circle \[=\pi {{r}^{2}}\]
A circle can be divided into 4 equal quarters. Thus the area of each quarter will be \[{{{}^{1}/{}_{4}}^{th}}\] of the area of the circle.
\[\therefore \]Area of one quarter \[=\dfrac{1}{4}\times \] area of circle
Area of quarter \[=\dfrac{\pi {{r}^{2}}}{4}\]
Thus the area of quarter OACB \[=\dfrac{1}{4}\times \pi {{r}^{2}}\].
We know that r = 3.5 cm.
Area of quarter OACB \[=\dfrac{1}{4}\pi \times {{\left( 3.5 \right)}^{2}}\]\[=\dfrac{1}{4}\times \dfrac{22}{7}\times 3.5\times 3.5=9.625c{{m}^{2}}.\]
From the figure, we can say that \[\angle AOD={{90}^{\circ }}\].
Now let us find the area of \[\Delta AOD.\]
We know that the area of a triangle \[=\dfrac{1}{2}\times base\times height\]
Here, base = OA = 3.5 cm and height = OD = 2 cm.
\[\therefore \]Area of \[\Delta AOD=\dfrac{1}{2}\times OD\times OA=\dfrac{1}{2}\times 2\times 3.5=3.5c{{m}^{2}}.\]
Hence, area of triangle AOD \[=3.5c{{m}^{2}}.\]
Thus to get the area of the shaded portion, we need to subtract the area of \[\Delta AOD\] from the area of quarter OACB.
Area of shaded portion = Area of quarter OACB – Area of \[\Delta AOD=9.625 - 3.5=6.125c{{m}^{2}}.\]
Thus we got the required area as \[6.125c{{m}^{2}}.\]

Note: We have found the area of the quarter as $ \dfrac{1}{4}\times{\pi{{r}^{2}}} $ . But the quarter can also be considered as the sector of a circle. The central angle is \[{{90}^{\circ }}\]. Thus by the sector formula, we can find the area of OACB. Sector formula \[=\dfrac{\theta }{360}\times \pi {{r}^{2}}\]. We know \[\theta ={{90}^{\circ }}\], i.e. \[\angle AOD={{90}^{\circ }}\]
\[\therefore \]Area of sector OACB \[=\dfrac{90}{360}\pi {{r}^{2}}=\dfrac{1}{4}\pi {{r}^{2}}\], which is equal to the area of one quarter of a circle.