Question

In the figure, \[AGB\], \[CGD\], \[EGF\]are straight lines. Find\[\left| \!{\underline {\,
  y \,}} \right. \].

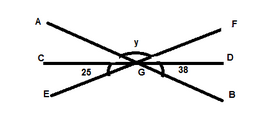
\[\begin{align}
  & \left( A \right){{97}^{\circ }} \\
 & \left( B \right){{127}^{\circ }} \\
 & \left( C \right){{100}^{\circ }} \\
 & \left( D \right){{117}^{\circ }} \\
\end{align}\]

Answer 1

Hint: In order to solve this question, we are going to use the properties of intersecting lines and of the angles at which they intersect. The vertically opposite angles are equal and the sum of the angles that lie on the same line is \[{{180}^{\circ }}\].

Complete step by step solution:
Starting off, with the lines \[EF\] and \[CD\],
The angles \[CGE\] and \[FGD\] are vertically opposite angles and hence they are equal,
i.e. \[\left| \!{\underline {\,
  CGE \,}} \right. =\left| \!{\underline {\,
  FGD \,}} \right. ={{25}^{\circ }}\]
and \[\left| \!{\underline {\,
  DGB \,}} \right. ={{38}^{\circ }}\]
now as the angles lying on the line \[AB\] form a linear angle , i.e. their sum is \[180{}^\circ \]
Therefore,
 \[\begin{align}
  & y+{{25}^{\circ }}+{{38}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow y+{{63}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow y={{180}^{\circ }}-{{63}^{\circ }} \\
 & \Rightarrow y={{117}^{\circ }} \\
\end{align}\]
So, the correct answer is “$y={{117}^{\circ }}$”.

Note: Alternatively, we can consider the straight line \[EF\], and take the three angles on this line, forming a linear angle
i.e.
 \[\begin{align}
  & \left| \!{\underline {\,
  FGA \,}} \right. =y \\
 & \left| \!{\underline {\,
  AGC \,}} \right. =\left| \!{\underline {\,
  DGB \,}} \right. ={{38}^{\circ }} \\
 & \left| \!{\underline {\,
  CGE \,}} \right. ={{25}^{\circ }} \\
\end{align}\]
Now, as we know that, the sum of these angles will be \[180{}^\circ \]
Therefore,
 \[\begin{align}
  & \left| \!{\underline {\,
  FGA \,}} \right. +\left| \!{\underline {\,
  AGC \,}} \right. +\left| \!{\underline {\,
  CGE \,}} \right. = \\
 & \Rightarrow y+{{38}^{\circ }}+{{25}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow y+{{63}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow y={{180}^{\circ }}-{{63}^{\circ }} \\
 & \Rightarrow y={{117}^{\circ }} \\
\end{align}\]
Thus, the above question can be solved in both the ways. Similarly, by considering the third line segment i.e. \[CD\] , the question can be solved in the same way as we know the value of both the angles, and the value of angle \[y\] can be calculated by subtracting their sum from \[180{}^\circ \].