Question

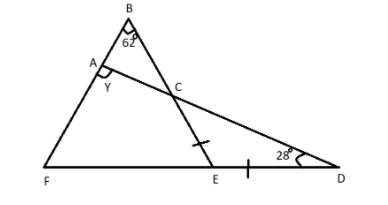
In the figure, ADF and BEF are triangles and $EC = ED$, find Y.

A) ${90^ \circ }$
B) ${91^ \circ }$
C) ${92^ \circ }$
D) ${93^ \circ }$

Answer 1

Hint:
We have given that ADF and BEF are triangles and $EC = ED$.
Using the Exterior angle property of $\Delta ABC$ find $\angle y$.

Complete step by step solution:
Here, we have given that ADF and BEF are triangles and $EC = ED$.
So, we have to find the value of Y
It is given in the question that $EC = ED$.
So, In $\Delta CDE$,
$\angle EDC = \angle ECD = {28^ \circ }$ (Angles opposite to equal sides are also equal)
$\angle ACB = \angle ECD = {28^ \circ }$ (Vertically opposite angles in a $\Delta ABC$)
We know,
$\angle y = \angle ACB + {62^ \circ }$ _ (Exterior angle property of $\Delta ABC$)
$\therefore \angle y = {28^ \circ } + {62^ \circ }$

$\therefore \angle y = {90^ \circ }$

Note:
Angles opposite to equal sides are also equal: Angles opposite to equal sides of an isosceles triangle are equal. The sides opposite to equal angles of a triangle are equal.
Vertically opposite angles: Vertically opposite angles are the angles opposite each other when two lines cross. Vertical in this case means they share the same vertex (corner point), not the usual meaning of up-down.

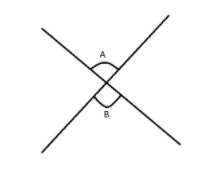
In the figure given above $\angle A$and $\angle B$are vertically opposite angles.