Question

In the figure above (not to scale) ABCD is trapezium in which $ \overline {AB} \parallel \overline {CD,} \;{\text{AD = CD}} $ and $ AB = 2CD $
If $ \angle ADC = 100^\circ $ then find $ \angle ABC $

Answer 1

Hint: First of all we will redraw the figure and mention all the given data. Also, will assume the measure of the side AD to be “x” and then will find the required angle using the properties of the different quadrilaterals and the triangles.

Complete step-by-step answer:

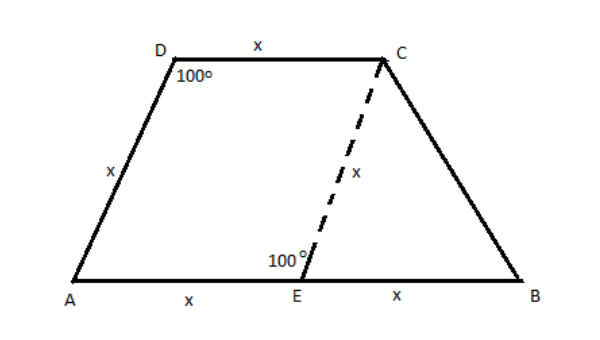
Let us assume the measure of the length of AD to be “x”
Given that:
 $
  AD = CD \\
  AD = CD = x \;
  $
Now, the framed quadrilateral is the Rhombus where the opposite sides are equal in it.
Therefore, $ AE = EC = AD = CD = x $
Since given that $ \angle ADC = 100^\circ $
By the congruent property SAS (side angle side) in the rhombus, opposite angles are equal.
 $ \Rightarrow \angle AEC = 100^\circ $
Also, given that $ AB = 2CD $
 $ \Rightarrow EC = x $
Now, $ \angle AEC $ and $ \angle BEC $ are supplementary angles since they share the same line.
The sum of supplementary angles is always one hundred and eighty degrees.
 $ \angle AEC + \angle BEC = 180^\circ $
Place the known value in the above expression –
 $ 100^\circ + \angle BEC = 180^\circ $
Make the required angle the subject and move other terms on the opposite sides. When you move any term from one side to the other then the sign of the term changes. Positive term becomes negative and vice-versa.
 $ \angle BEC = 180^\circ - 100^\circ $
Simplify finding the difference of the terms in the above expression –
 $ \angle BEC = 80^\circ $ …. (A)
Now, In $ \Delta BEC $
Since the opposite sides are equal, $ \angle EBC = \angle ECB $ …. (B)
In any triangle sum of all three angles is equal to $ 180^\circ $
 $ \therefore \angle EBC + \angle ECB + \angle BEC = 180^\circ $
Place the known values in the above expression –
 $ \therefore \angle EBC + \angle EBC + 80^\circ = 180^\circ $ (from A & B)
Simplify the above expression –
 $ \therefore 2\angle EBC = 180^\circ - 80^\circ $
 $ \therefore 2\angle EBC = 100^\circ $
Term multiplicative on one side if moved to the opposite side then it goes to the denominator.
 $
  \therefore \angle EBC = \dfrac{{100^\circ }}{2} \\
  \therefore \angle EBC = 50^\circ \;
  $
Hence, the required $ \angle ABC = 50^\circ $
So, the correct answer is “ $ \angle ABC = 50^\circ $ ”.

Note: Always remember different properties of the quadrilaterals and its types. Refer to the other congruence property for the different combinations of sides and angles. Always remember the sum of the angles in the triangle is one hundred and eighty and the sum of the angles in the quadrilateral is three hundred and sixty.