
In the figure above (not to scale), ABCD is a rectangle with the diagonals intersecting at O. If $OA=AB$ and $\angle AEC={{120}^{\circ }}$ then $\angle OAF$ is
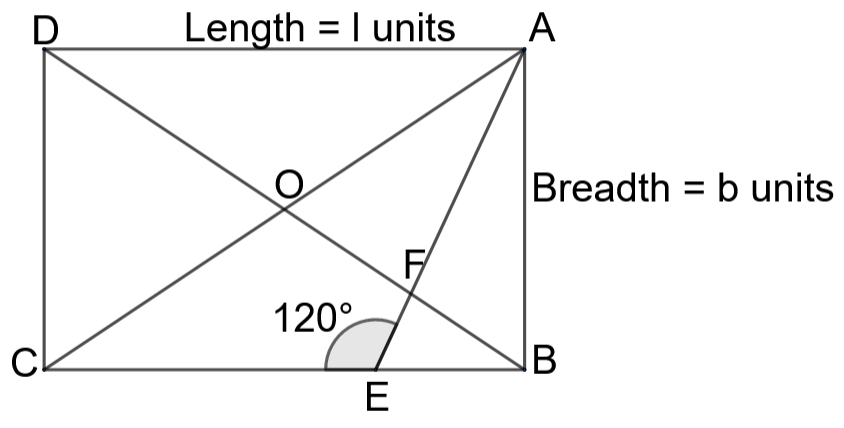
A. ${{30}^{\circ }}$
B. ${{45}^{\circ }}$
C. ${{60}^{\circ }}$
D. ${{75}^{\circ }}$

Answer
587.7k+ views
Hint: To solve this question, we should use the formulae related to rectangles. We know that the diagonals of a rectangle bisect each other. Using this property, we can write that $OA=\dfrac{AC}{2}$. We know that a right angled triangle ABC with the sides a, b, c where c is the hypotenuse, the relation between a, b, c is ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$. We can apply this in the triangle ABC and get a relation between the length and the breadth. Using $\angle AEC={{120}^{\circ }}$, we can get the value of $\angle AEB$ and using this, we can get the value of $\angle EAB$from the triangle $\Delta EAB$. We know that $\tan \left( \angle CAB \right)=\dfrac{Length}{Breadth}\Rightarrow \angle CAB={{\tan }^{-1}}\left( \dfrac{Length}{Breadth} \right)$. The difference of the angles $\angle CAB$ and $\angle EAB$ gives the required angle.
Complete step by step answer:
Let us consider the length and breadth of the given rectangle as l and b respectively.
We know that a right angled triangle ABC with the sides a, b, c where c is the hypotenuse, the relation between a, b, c is ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$.
Let us consider the $\Delta ABC$. We have the side AC as the hypotenuse and the sides AB and BC are the other sides. We can write that
$\begin{align}
& A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\
& A{{C}^{2}}={{l}^{2}}+{{b}^{2}} \\
\end{align}$
We know that the diagonals of a rectangle bisect each other. Using this, we can write that
$OA=\dfrac{AC}{2}$
But we can write from the question that $OA=AB=b$
Using this, we get
$\begin{align}
& \dfrac{AC}{2}=b \\
& AC=2b \\
\end{align}$
Using this, we get
$\begin{align}
& {{\left( 2b \right)}^{2}}={{l}^{2}}+{{b}^{2}} \\
& 4{{b}^{2}}={{l}^{2}}+{{b}^{2}} \\
& {{l}^{2}}=3{{b}^{2}} \\
& l=\sqrt{3}b \\
\end{align}$
In the $\Delta ABC$
$\tan \left( \angle CAB \right)=\dfrac{l}{b}$
From the above relation, we can write that
$\tan \left( \angle CAB \right)=\dfrac{l}{b}=\sqrt{3}$
By taking inverse, we get
$\angle CAB={{\tan }^{-1}}\sqrt{3}={{60}^{\circ }}$
Let us consider the point E. The sum of the two angles at the point E should be equal to ${{180}^{\circ }}$. We can write it as
$\angle AEC+\angle AEB={{180}^{\circ }}$
Using $\angle AEC={{120}^{\circ }}$, we get
$\begin{align}
& {{120}^{\circ }}+\angle AEB={{180}^{\circ }} \\
& \angle AEB={{60}^{\circ }} \\
\end{align}$
From the right angled triangle $\Delta AEB$, we can write that
$\angle AEB+\angle EAB={{90}^{\circ }}$
Using the above value, we can write that
$\begin{align}
& {{60}^{\circ }}+\angle EAB={{90}^{\circ }} \\
& \angle EAB={{30}^{\circ }} \\
\end{align}$
From the diagram at the point A, we can write that
$\angle OAF+\angle EAB=\angle CAB$
By substituting the values, we get
$\begin{align}
& \angle OAF+{{30}^{\circ }}={{60}^{\circ }} \\
& \angle OAF={{60}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }} \\
\end{align}$
$\therefore $The required angle is $\angle OAF={{60}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }}$.
So, the correct answer is “Option A”.
Note: Some students try to use the relations that $\angle OAF=\angle CAB-{{30}^{\circ }}$ and $\tan \left( \angle CAB \right)=\sqrt{3}$ apply tangent on both sides and try to calculate the value further. This calculation also leads to the answer but it will be lengthier than the method that we followed. So, the trick to solve this type of questions easily is to calculate the angles and apply the formulae.
Complete step by step answer:
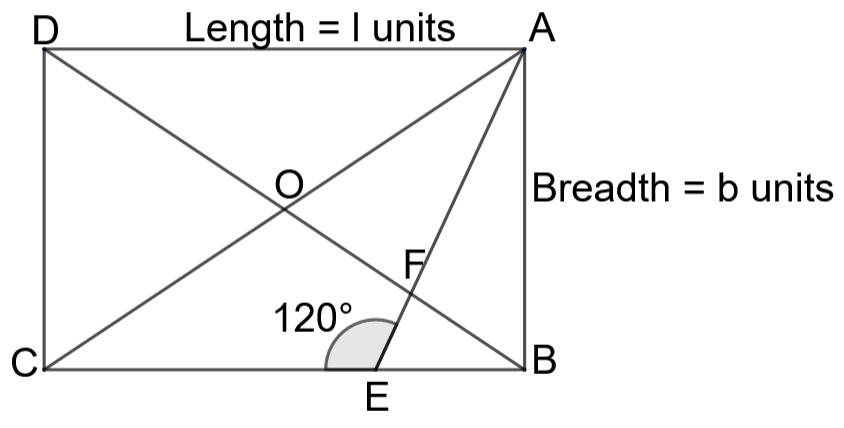
Let us consider the length and breadth of the given rectangle as l and b respectively.

We know that a right angled triangle ABC with the sides a, b, c where c is the hypotenuse, the relation between a, b, c is ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$.
Let us consider the $\Delta ABC$. We have the side AC as the hypotenuse and the sides AB and BC are the other sides. We can write that
$\begin{align}
& A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\
& A{{C}^{2}}={{l}^{2}}+{{b}^{2}} \\
\end{align}$
We know that the diagonals of a rectangle bisect each other. Using this, we can write that
$OA=\dfrac{AC}{2}$
But we can write from the question that $OA=AB=b$
Using this, we get
$\begin{align}
& \dfrac{AC}{2}=b \\
& AC=2b \\
\end{align}$
Using this, we get
$\begin{align}
& {{\left( 2b \right)}^{2}}={{l}^{2}}+{{b}^{2}} \\
& 4{{b}^{2}}={{l}^{2}}+{{b}^{2}} \\
& {{l}^{2}}=3{{b}^{2}} \\
& l=\sqrt{3}b \\
\end{align}$
In the $\Delta ABC$
$\tan \left( \angle CAB \right)=\dfrac{l}{b}$
From the above relation, we can write that
$\tan \left( \angle CAB \right)=\dfrac{l}{b}=\sqrt{3}$
By taking inverse, we get
$\angle CAB={{\tan }^{-1}}\sqrt{3}={{60}^{\circ }}$
Let us consider the point E. The sum of the two angles at the point E should be equal to ${{180}^{\circ }}$. We can write it as
$\angle AEC+\angle AEB={{180}^{\circ }}$
Using $\angle AEC={{120}^{\circ }}$, we get
$\begin{align}
& {{120}^{\circ }}+\angle AEB={{180}^{\circ }} \\
& \angle AEB={{60}^{\circ }} \\
\end{align}$
From the right angled triangle $\Delta AEB$, we can write that
$\angle AEB+\angle EAB={{90}^{\circ }}$
Using the above value, we can write that
$\begin{align}
& {{60}^{\circ }}+\angle EAB={{90}^{\circ }} \\
& \angle EAB={{30}^{\circ }} \\
\end{align}$
From the diagram at the point A, we can write that
$\angle OAF+\angle EAB=\angle CAB$
By substituting the values, we get
$\begin{align}
& \angle OAF+{{30}^{\circ }}={{60}^{\circ }} \\
& \angle OAF={{60}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }} \\
\end{align}$
$\therefore $The required angle is $\angle OAF={{60}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }}$.
So, the correct answer is “Option A”.
Note: Some students try to use the relations that $\angle OAF=\angle CAB-{{30}^{\circ }}$ and $\tan \left( \angle CAB \right)=\sqrt{3}$ apply tangent on both sides and try to calculate the value further. This calculation also leads to the answer but it will be lengthier than the method that we followed. So, the trick to solve this type of questions easily is to calculate the angles and apply the formulae.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




