Question

In the figure, \[ABCDEF\] is a regular hexagon, and its center is point \[O\]. What is the value of \[x\].

A) \[80^\circ \]
B) \[60^\circ \]
C) \[40^\circ \]
D) \[30^\circ \]

Answer 1

Hint:
 We are required to find the value of \[x\] in the given figure. We will use the concept of the equilateral triangles to find the angle. For that we will prove all the sides of the triangle formed equal using the concepts of the geometry.
Formula Used: We will use the formula of the interior angle, \[{\rm{Interior angle}} = \dfrac{{\left[ {n - 2} \right]180}}{n}\], where \[n\] is the number of sides or number of angles of a polygon.

Complete step by step solution:
We have to find the value of the unknown angle \[x\] in the given figure. The unknown angle \[x\] is an angle of a polygon \[BCDO\].
Let us divide \[BCDO\] into two triangles.

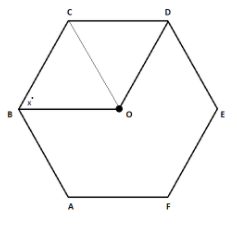
Now we know that \[BCDO\] will be a parallelogram with all sides equal. This means that \[BCDO\] is a rhombus. This is because \[BC = CD\]. As it is given that the hexagon is regular so all the sides will be equal.
Now, since our hexagon is regular, the side \[OD\] should be equal and parallel to the side \[BC\]. Since our hexagon is regular so side \[CD\] should be equal and parallel to side \[OB\].
As \[BC\] and \[CD\] are equal, and \[CD = BO\], and \[BC = OD\], then by corollary all the sides are equal.
Also, \[OB = OC\]. This is because in the regular hexagon, all the corners are equidistant from the center. Hence, we can conclude that \[BC = CO = OB\].
This implies that \[\Delta BCO\] is an equilateral triangle.
Now, we know that in an equilateral triangle all angles are \[60^\circ \]. So, \[x\] should be equal to \[60^\circ \], as it is in the angle of the equilateral triangle.

As this answer matches with option [B], so this is the correct option.

Note:
The alternate way to solve this question can be as follows.
Since, we are given a regular hexagon so we will find the degree measure of each of its interior angles.
Since, we are provided with a hexagon so \[n = 6\].
We will substitute \[n = 6\] into the formula \[{\rm{Interior angle}} = \dfrac{{\left[ {n - 2} \right]180}}{n}\].
\[\begin{array}{c}{\rm{Interior angle}} = \dfrac{{\left[ {n - 2} \right]180}}{n}\\ = \dfrac{{\left[ {6 - 2} \right]180}}{6}\end{array}\]
Subtracting the terms and simplifying the expression, we get
\[\begin{array}{c}{\rm{Interior angle}} = \dfrac{{4 \times 180}}{6}\\ = 120^\circ \end{array}\]
Hence, each angle of the hexagon is of \[120^\circ \].
Now, as \[OB\] is a line joining the center and the corner, hence, \[OB\] bisects \[\angle CBA\].
And as \[\angle CBA\] is \[120^\circ \], so \[x\] will be
\[\begin{array}{c}x = \dfrac{{120^\circ }}{2}\\ = 60^\circ \end{array}\]
\[\therefore\] \[x\] is equal to \[60^\circ \].