Question

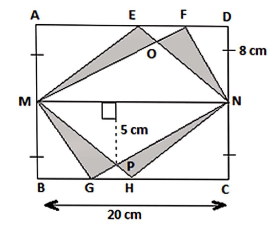
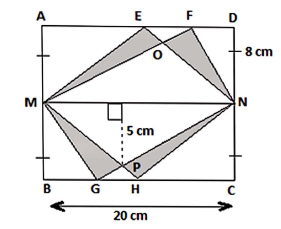
In the figure, $ABCD$ is rectangle and line $MN$ cuts the rectangles into half. Triangle $MNO$ and triangle $MNP$ are identical triangles. The area of shaded region is

A. More than $180c{m^2}$
B. Equal to $120c{m^2}$
C. More than $120c{m^2}$
D. Less than $120c{m^2}$

Answer 1

Hint: In this question, we have to find out the value of shaded area. To find this, work out the area of the total triangle i.e. total area of $\Delta MNF,\Delta MNE,\Delta MHC$ & $\Delta MGN$ and sum there are.
Again, take out the total area of $\Delta MON$ & $\Delta MPN$. To solve the area of the shaded region, subtract their area. Their difference is the required area of the shaded region.

Complete step-by-step answer:
We know that,
When two triangles lie between two parallel lines with the same base, then the area of triangles is equal.
$\therefore $Area of $\Delta MNF = $area of $\Delta MNE..........(i)$
Since – $ABCD$is a rectangle with length$ = 20cm$and breadth $16cm$.
And $MN$divides the rectangle in two halves.
Then area of rectangle $AMND = $Area of rectangle $MBCN$.
$\therefore $$\Delta MNF,\Delta MNE,\Delta MNG$and $\Delta MNH$are identical, i.e. their area will also be the same.
$\therefore $Area of $(\Delta MNF + \Delta MNE + \Delta MNG + \Delta MNH)$
$ = 4 \times \left( {\dfrac{1}{2} \times b \times h} \right)$
Height of $\Delta MNF$$ = $breadth of rectangle $AMND$-
$\therefore $$\therefore h = 8cm$
& $b = 20cm$(length of rectangle)
$\therefore $Area of $(\Delta MNF + \Delta MNE + \Delta MNG + \Delta MNH)$
$ = 4 \times \dfrac{1}{2} \times 20 \times 8 = 320c{m^2}$.
Again,
Area of $\left( {\Delta MON + \Delta MPN} \right) = \dfrac{1}{2} \times {b_1} \times {h_1}$
$\therefore $Base of $\Delta MON$$ = 20cm$
Height of $\Delta MON$$ = 5cm$(given)
& given, $\Delta MON$and $\Delta MPN$ are identical.
$\therefore $Area of $\left( {\Delta MON + \Delta MPN} \right) = \left( {\dfrac{1}{2} \times 20 \times 5} \right) \times 4 = 200c{m^2}$
[Since $\Delta MON$ lies both in $\Delta MNF$ & $\Delta MEN$ and $\Delta MPN$ lies both in $\Delta MHN$ & $\Delta MGN$].
Area of shaded region $ = $Area of $\left( {\Delta MNF + \Delta MNE + \Delta MNG + \Delta MNH} \right)$$ - $Area of $\left( {\Delta MON + \Delta MPN} \right)$$ = \left( {320 - 200} \right)c{m^2} = 120c{m^2}$

Option B is the correct answer.

Note: This is a type of question from geometry. For this question one should know the theorem –
“Area of triangles lying between two parallel lines and the same base are equal”. So, for solving questions, theorems are very important. Using theorems, this type of question is easy to solve.