Question

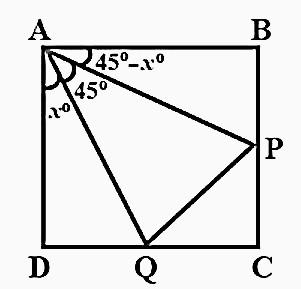
In the figure, ABCD is a square of side 1 dm and $\angle PAQ={{45}^{0}}$ . The perimeter (in dm) of the triangle PQC is.

(a) $2$
(b) $1+\sqrt{2}$
(c) $2\sqrt{2}-1$
(d) $1+\sqrt{3}$

Answer 1

Hint:For solving this question we will find the length of each side of the triangle PQC with the help of concepts of trigonometry and two algebraic identities of the whole square formula. Then, with the proper application of formulas and some concepts of geometry, we will solve for the correct answer.

Complete step-by-step answer:
Given:
We have a figure of square ABCD of side 1 dm and $\angle PAQ={{45}^{0}}$ . We have to find the perimeter of $\Delta PQC$ . The figure is given below:

Now, let $\angle QAD={{x}^{0}}$ then, $\angle BAP={{45}^{0}}-{{x}^{0}}$ .
We will use the following formulae in solving this question:
$\begin{align}
  & \tan {{45}^{0}}=1..................\left( 1 \right) \\
 & \tan \left( A-B \right)=\dfrac{\tan A-\tan B}{1+\tan A\cdot \tan B}...............\left( 2 \right) \\
 & \left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}.........................\left( 3 \right) \\
 & {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab.........................\left( 4 \right) \\
 & {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab.........................\left( 5 \right) \\
\end{align}$
Now, as ABCD is a square, so $AB=BC=CD=AD=1$ dm. Then,
\[\begin{align}
  & \text{In the }\Delta ADQ\text{ ,} \\
 & \tan x=\dfrac{DQ}{AD} \\
 & \Rightarrow DQ=AD\tan x \\
 & \Rightarrow DQ=\tan x \\
 & \text{In the }\Delta ABP\text{ ,} \\
 & \tan \left( {{45}^{0}}-x \right)=\dfrac{BP}{AB} \\
 & \Rightarrow BP=AB\tan \left( {{45}^{0}}-x \right) \\
 & \Rightarrow BP=\tan \left( {{45}^{0}}-x \right) \\
\end{align}\]
Now, we know that $DC=DQ+QC=1$ and $BC=BP+PC=1$ . Then,
\[\begin{align}
  & DQ+QC=1 \\
 & \Rightarrow \tan x+QC=1 \\
 & \Rightarrow QC=1-\tan x..............\left( 6 \right) \\
 & BP+PC=1 \\
 & \Rightarrow \tan \left( {{45}^{0}}-x \right)+PC=1 \\
 & \Rightarrow PC=1-\tan \left( {{45}^{0}}-x \right)............\left( 7 \right) \\
\end{align}\]
Now, use the formula from the equation (1) and (2) in the equation (7). Then,
\[\begin{align}
  & PC=1-\tan \left( {{45}^{0}}-x \right) \\
 & \Rightarrow PC=1-\dfrac{\tan {{45}^{0}}-\tan x}{1+\tan {{45}^{0}}\cdot \tan x} \\
 & \Rightarrow PC=1-\dfrac{1-\tan x}{1+\tan x} \\
 & \Rightarrow PC=\dfrac{2\tan x}{1+\tan x}............\left( 8 \right) \\
\end{align}\]
Now, before proceeding further just take a look at the result of the Pythagoras Theorem. The Pythagoras Theorem states that in a right-angled triangle as shown below $\Delta ABC$ , the square of the hypotenuse is equal to the sum of the squares of the other two sides.

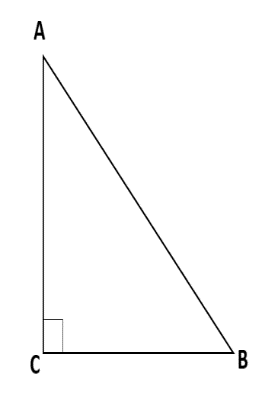
In the $\Delta ABC$ , $\angle ACB={{90}^{0}}$ and AB is the hypotenuse, BC is the base and AC is the perpendicular. From Pythagoras Theorem, we have:
${{\left( BC \right)}^{2}}+{{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}$
Then, we can write, ${{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$ .

Now, as in $\Delta PCQ$ , $\angle PCQ={{90}^{0}}$ and the side $PQ$ is the hypotenuse. So, we can apply the result of Pythagoras theorem in $\Delta PCQ$ . Then,
${{\left( PQ \right)}^{2}}={{\left( PC \right)}^{2}}+{{\left( QC \right)}^{2}}$
Now, put \[QC=1-\tan x\] from equation (6) and \[PC=\dfrac{2\tan x}{1+\tan x}\] from equation (8) in the above equation. Then,
$\begin{align}
  & {{\left( PQ \right)}^{2}}={{\left( 1-\tan x \right)}^{2}}+{{\left( \dfrac{2\tan x}{1+\tan x} \right)}^{2}} \\
 & \Rightarrow {{\left( PQ \right)}^{2}}=\dfrac{{{\left( 1-\tan x \right)}^{2}}{{\left( 1+\tan x \right)}^{2}}+4{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}} \\
\end{align}$
Now, use the formula written in the equation (3), equation (4) and equation (5) in the above equation. Then,
$\begin{align}
  & {{\left( PQ \right)}^{2}}=\dfrac{{{\left( 1-\tan x \right)}^{2}}{{\left( 1+\tan x \right)}^{2}}+4{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}}=\dfrac{{{\left[ \left( 1-\tan x \right)\left( 1+\tan x \right) \right]}^{2}}+4{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}} \\
 & \Rightarrow {{\left( PQ \right)}^{2}}=\dfrac{{{\left[ 1-{{\tan }^{2}}x \right]}^{2}}+4{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}}=\dfrac{1+{{\tan }^{4}}x-2{{\tan }^{2}}x+4{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}} \\
 & \Rightarrow {{\left( PQ \right)}^{2}}=\dfrac{1+{{\left( {{\tan }^{2}}x \right)}^{2}}+2{{\tan }^{2}}x}{{{\left( 1+\tan x \right)}^{2}}}=\dfrac{{{\left( 1+{{\tan }^{2}}x \right)}^{2}}}{{{\left( 1+\tan x \right)}^{2}}}={{\left[ \dfrac{1+{{\tan }^{2}}x}{1+\tan x} \right]}^{2}} \\
\end{align}$
$\Rightarrow PQ=\dfrac{1+{{\tan }^{2}}x}{1+\tan x}...................\left( 9 \right)$
Now, we have calculated the length of all sides of triangle PQC. From equation (6), (8) and (9). Then,
$\begin{align}
  & PQ+PC+QC \\
 & \Rightarrow \dfrac{1+{{\tan }^{2}}x}{1+\tan x}+\dfrac{2\tan x}{1+\tan x}+1-\tan x \\
 & \Rightarrow \dfrac{1+{{\tan }^{2}}x+2\tan x}{1+\tan x}+1-\tan x \\
 & \Rightarrow \dfrac{{{\left( 1+\tan x \right)}^{2}}}{\left( 1+\tan x \right)}+1-\tan x \\
 & \Rightarrow 1+\tan x+1-\tan x \\
 & \Rightarrow 2 \\
\end{align}$
Now, from the above calculation, we can say that the perimeter of triangle PQC will be 2 dm.
Hence, (a) is the correct option.

Note: Here, the student should use the geometrical properties of the square and we should know how to apply Pythagoras Theorem in case of any right-angled triangle and then apply every formula very carefully and avoid calculation mistakes while solving to get the correct answer.