Question

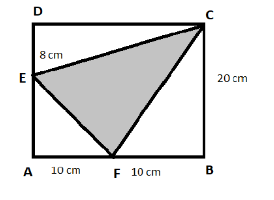
In the figure ABCD, find the area of the shaded region.

Answer 1

Hint: The shaded region is a triangle inscribed in a square. Its area can’t be calculated directly so we will be calculating the area of triangles of non-shaded triangles from the area of the square
Area of square = ${a^2}$ where, a is side of square
Area of triangle = $\dfrac{1}{2} \times b \times h$

Complete step-by-step answer:
Required area of shaded region:
Area of square (ABCD) – Sum of areas of three triangles (AEF + BCF + DEC) _________ (1)
From the figure,
AB = BC = CD = DA = 20 cm [all sides of square is equal]
AF = FB = 10 cm [Given]
🡪 Calculating area of square ABCD :
Side of square (a) = 20 cm
Area of square (${a^2}$)
= ${\left( {20} \right)^2}$
= 400
Therefore, the area of square is 400 $c{m^2}$
🡪 Calculating area of the 3 triangles :
i) $ar(\vartriangle AEF)$ = $\dfrac{1}{2} \times b \times h$
= $\dfrac{1}{2} \times AF \times AE$
AF = 10 cm (Given)
AE = 12 cm [20 (AD) – 8 (ED) and AE = AD - ED]
Substituting:
= $\dfrac{1}{2} \times 10 \times 12$
= 60
Therefore, the area of triangle AEF is $60c{m^2}$.
ii) $ar(\vartriangle BCF)$= $\dfrac{1}{2} \times b \times h$
= $\dfrac{1}{2} \times BF \times CB$
BF = 10 cm
CB = 20 cm
Substituting:
= $\dfrac{1}{2} \times 10 \times 20$
= 100
Therefore, the area of triangle BCF is $100c{m^2}$
iii) $ar(\vartriangle DEC)$= $\dfrac{1}{2} \times b \times h$
= $\dfrac{1}{2} \times DC \times DE$
DC = 20 cm
 DE = 8 cm
 Substituting:
= $\dfrac{1}{2} \times 20 \times 8$
= 80
Therefore, the area of triangle DEC is $80c{m^2}$
Substituting the obtained values in (1), we get:
Area of square (ABCD) – Sum of areas of three triangles (AEF + BCF + DEC)
400 – (100 + 60 + 80)
400 – 240 = 160
Therefore, the required area of the shaded region is calculated to be $160c{m^2}$.

Note: In such questions, where the required region cannot be calculated directly, we can find the area of smaller figures (lying in a non-required region, calculated easily) and then subtract these areas from the main larger figure.