Question

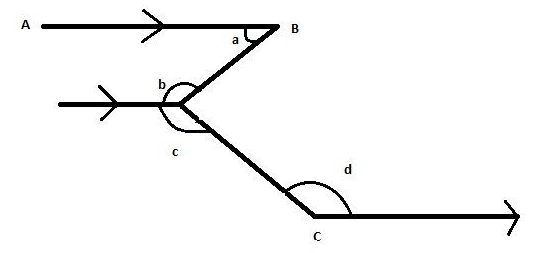
In the figure, AB is parallel to CD, which of the following is true?
A) $a + b = {180^{\circ}}$
B) $b + c = {180^{\circ}}$
C) $c + d = {180^{\circ}}$
D) $a + b + c = {180^{\circ}}$

Answer 1

Hint:
In a given Statement we have AB is parallel to CD. As we know that two lines are parallel if they never intersect each other. So, AB and CD will not intersect each other. Now to check whether the given statement is true or not use properties of lines to solve it. We use consecutive interior angles of lines.

Complete step by step solution:
Now we have given that the AB is parallel to line CD. Extending CD to point p
Since AB is parallel to CD. AB will be parallel to CP. There is a line in the middle of the
line AB and CD. Thus the middle is parallel to both the line AB and CD showing in the figure.

Let us name this middle line EF.

Now as EE is parallel to AB and angles a, b are consecutive interior angles. Since the sum of consecutive interior angles of the parallel lines is equal to 180 degrees. So, the sum of angle a and angle b is ${180^{\circ}}$.
Therefore $a + b = {180^{\circ}}$

Option (A) is correct.

Note:
When a transversal intersects two or more parallel lines in the same place a series, a series of angles formed. Certain pairs of angles are given specific names that must base upon their certain locations in relation to the lines. The angle located on the same side of the transverse and interior of the parallel times then is called consecutive interior angles.