Question

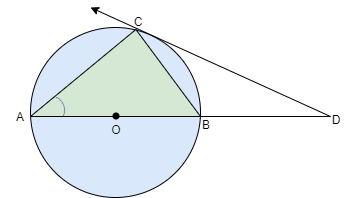
In the figure, AB is a diameter and AC is the chord of a circle such that$\angle BAC = {30^ \circ }$. If DC is a tangent, then $\Delta BCD$ is

A. Isosceles
B. Equilateral
C. Right angled
D. Acute angled

Answer 1

Hint: In this question remember to join point O to C and use $\angle $ACB is equal to ${90^ \circ }$ by property of diameter, using these instructions will help you to approach closer towards the solution to the problem.

Complete step by step solution:
According to the given information we have circle with diameter AB which have a triangle ABC inscribed inside the circle with cord AC and DC is the tangent and also one of the angle of triangle i.e.$\angle BAC = {30^ \circ }$
Now joining point O to C

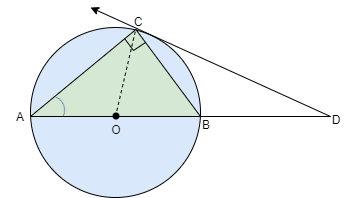
By the property of diameter of circle $\angle $ACB = ${90^ \circ }$
In triangle ABC by angle sum property
$\angle $BAC + $\angle $ACB + $\angle $CBA = ${180^ \circ }$
Substituting the given values in the above equation
${30^ \circ }$ + ${90^ \circ }$+ $\angle $CBA = ${180^ \circ }$
$ \Rightarrow $$\angle $CBA = ${180^ \circ }$ – ${120^ \circ }$
$ \Rightarrow $$\angle $CBA = ${60^ \circ }$
In the triangle OBC
CO = BO since CO and BO are the radius of circle
Since the side CO = BO therefore $\angle $OCB = $\angle $OBC = ${60^ \circ }$ by the property of isosceles triangle
As we know that the point where tangent touches the circle is perpendicular to the radius of the circle
Therefore $\angle $OCB + $\angle $DCB = ${90^ \circ }$
Substituting the given values in the above equation we get
${60^ \circ }$ + $\angle $DCB = ${90^ \circ }$
$ \Rightarrow $$\angle $DCB = ${90^ \circ }$ – ${60^ \circ }$
$ \Rightarrow $$\angle $DCB = ${30^ \circ }$
Now In triangle BCD
We know that by the property of external angle $\angle $OBC = $\angle $DCB + $\angle $CDB
No substituting the given values in the above equation we get
${60^ \circ }$= ${30^ \circ }$+ $\angle $CDB
$ \Rightarrow $$\angle $CDB = ${60^ \circ }$ – ${30^ \circ }$
$ \Rightarrow $$\angle $CDB = ${30^ \circ }$
In triangle BCD by the angle sum property
$\angle $CDB + $\angle $DCB + $\angle $CBD = ${180^ \circ }$
Substituting the values in the above equation we get
${30^ \circ }$ + ${30^ \circ }$+ $\angle $CBD = ${180^ \circ }$
$ \Rightarrow $$\angle $CBD = ${180^ \circ }$ – ${30^ \circ }$ – ${30^ \circ }$
$ \Rightarrow $$\angle $CBD = ${180^ \circ }$ – ${60^ \circ }$
$ \Rightarrow $$\angle $CBD = ${120^ \circ }$
So in triangle BCD angles $\angle $CDB, $\angle $DCB and$\angle $CBD are${120^ \circ }$, ${30^ \circ }$ and ${30^ \circ }$
Since in triangle BCD $\angle $DCB = $\angle $CBD and $\angle $CDB therefore we can say that triangle BCD is an isosceles triangle
Hence option A is the correct option.

Note: In the above solution isosceles triangle was the correct answer because in isosceles triangle 2 angles are equal to each other this similar properties shown by the triangle BCD which made us to decide that it is a isosceles triangle and the reason that the triangle BCD was not a equilateral triangle, right angled triangle and acute angled triangle because in equilateral triangle all angles are equal to each other and in right angled triangle at least 1 angle of the triangle should be ${90^ \circ }$ and whereas in acute angled triangle all angles are less than ${90^ \circ }$ but these all properties of the triangle were not shown by the triangle BCD due to which these all triangles were not the correct option for this problem.