Question

In the figure, AB II CD, find x.

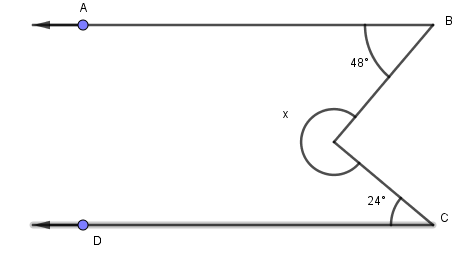
Answer 1

Hint: Draw a line parallel to AB and CD and use the concept and relations between angles when two parallel lines intersected by a transversal. By drawing parallel line angle x is divided into two parts, find each part and then add to get the value of x.

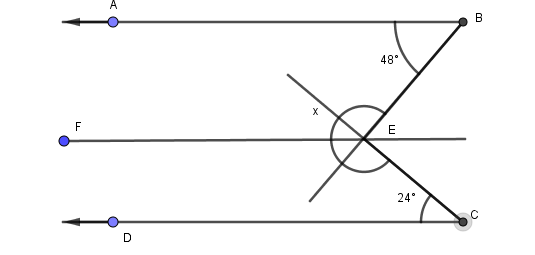
Complete step-by-step answer:
Put a point E associated with angle x as in figure. Draw a line FE parallel to AB and CD and pass through E.
Now, extend BE and CE as shown in figure.
AB and FE are parallel and BE is transversal.
Therefore, ∠ ABE + ∠ FEB = 180°
[If two lines are parallel and a transversal intersecting the two lines, then sum of interior angles on the same side of transversal is equal to 180°]
Given that ∠ ABE = 48°
⇒ 48° + ∠ FEB = 180° ⇒ ∠ FEB = 180° − 48° = 132°
Also, DC and FE are parallel and CE is transversal.
Therefore, ∠ DCE + ∠ FEC = 180°
[If two lines are parallel and a transversal intersecting the two lines, then sum of interior angles on the same side of transversal is equal to 180°]
Given that ∠ DCE = 24°
⇒ 24° + ∠ FEC = 180° ⇒ ∠ FEC = 180° − 24° = 156°
Now, ∠x = ∠ FEB + ∠ FEC = 132° + 156° = 288°
Therefore, ∠ x = 288°

Note: In these types of questions, draw the lines parallel of perpendicular whichever required to apply the theorem or concepts. You must know the parallel lines and it’s transversal to establish the relations between angles. You must use terms like alternate interior angle, corresponding angles, opposite angles etc.