Question

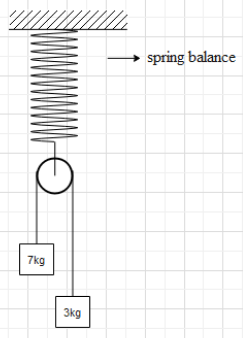
In the figure, a pulley of negligible weight is suspended by a spring balance S. Masses of 3kg and 7kg respectively are attached to opposite ends of a string passing over a pulley P. The spring balance reads:

A. equal to 10 kg
B. less than 10 kg
C. more than 10 kg
D. equal to 4kg

Answer 1

Hint: Suppose the tension in the spring is T. Then the reading (mass) of the spring balance is equal to $m=\dfrac{T}{g}$ , where g is the acceleration due to gravity. So, find the tension on the spring by analysing the forces acting on the two masses.

Formula used:
${{F}_{g}}=mg$
${{F}_{net}}=ma$
where $g$ is the acceleration due to gravity and $m$ be the mass.

Complete step by step answer:
A spring balance reads according to the tension caused in the spring.Suppose the tension in the spring is T. Then the reading (mass) of the spring balance is equal to $m=\dfrac{T}{g}$,
where g is the acceleration due to gravity.
Let the tension in the string over the pulley be T. Then tension in the spring will be $T+T=2T$.
The tension force T will drag both the masses in the upwards direction.Other than the tension force, the gravitational force will act on the masses in the downward direction.
The gravitational force on a mass m is given as ${{F}_{g}}=mg$
Therefore, the gravitational force on the 7kg mass is ${{F}_{g,1}}=7\times 10=70N$.
The gravitational force on the 3kg mass is ${{F}_{g,2}}=3\times 10=30N$.
Let the 7kg mass accelerate downwards and the 3 kg mass accelerate upwards with an acceleration $a$. Now, the free body of the two masses will look like:-

The net force on 7kg mass is ${{F}_{1}}={{F}_{g,1}}-T$.
And the net force on 3kg mass is ${{F}_{2}}=T-{{F}_{g,2}}$.
From Newton's second law of motion, ${{F}_{net}}=ma$.
This means that ${{F}_{1}}=7a$ and ${{F}_{2}}=3a$.
$7a={{F}_{g,1}}-T$ …. (i)
and $3a=T-{{F}_{g,2}}$ ….. (ii).
From (ii) we get that $a=\dfrac{T-{{F}_{g,2}}}{3}$
Substitute the value of a in (i).
$\Rightarrow 7\left( \dfrac{T-{{F}_{g,2}}}{3} \right)={{F}_{g,1}}-T$
Substitute the values of the gravitational forces.
$\Rightarrow 7\left( \dfrac{T-30}{3} \right)=70-T$
$\Rightarrow 7T-210=210-3T$
$\Rightarrow T=42N$.
$\therefore 2T=84N$
This means that tension in the spring is 84N.
Therefore, the spring balance the reading of the spring balance is,
$m=\dfrac{T}{g}\\
\Rightarrow m=\dfrac{T}{10}\\
\Rightarrow m=\dfrac{84}{10}\\
\therefore m=8.4kg$
Therefore, the reading in the spring balance is less than 10kg.

Hence, the correct option is B.

Note: Some students may perform a mistake by considering the system to be in equilibrium and the two masses to be at rest. The system will be in equilibrium only when the gravitational force acting on both masses are equal, i.e. when the two masses are equal.