Question

In the figure A and B are two blocks of mass 4kg and 2kg respectively attached to the two ends of a light string passing over a disc C of mass $40kg$ and radius $0.1m$. The disc is free to rotate about fixed horizontal axes, coinciding with its own axis. The system is released from rest and the string does not slip over the disc. Then,

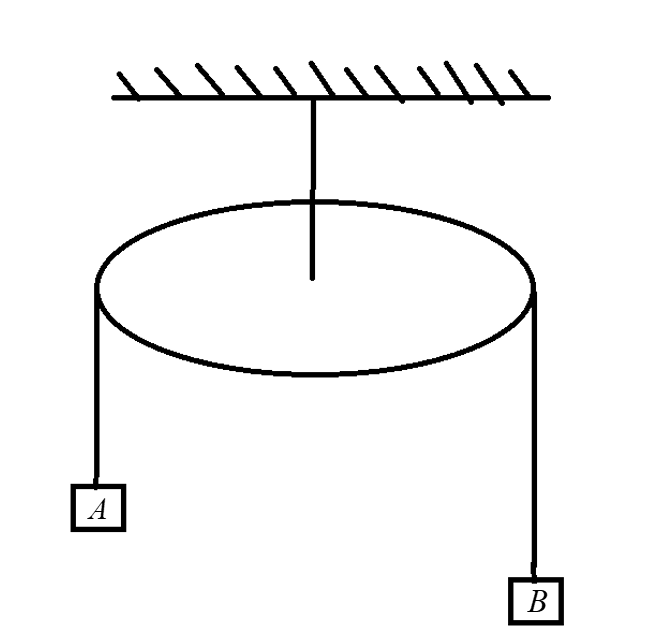
(This question has multiple correct options.)
A) The linear acceleration of mass B is $\dfrac{{10}}{{13}}\dfrac{m}{{{s^2}}}$
B) The number of revolutions made by the disc at the end of $10\sec $. from the start is $\dfrac{{5000}}{{26\pi }}$.
C) The tension in the string segment supporting the block A is $\dfrac{{480}}{{13N}}$.
D) None of these.

Answer 1

Hint: We know that weight depends on the direction because it is a vector quantity. the weight of an object is acting always toward the center of the earth.

Complete step by step answer:
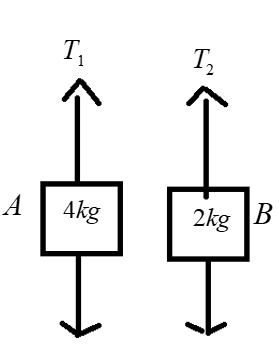
Block A has a higher weight than block B, so A will have a downward acceleration and B will in the upward direction of the same magnitude because of constrained, let ${T_1}{\text{and }}{{\text{T}}_2}$ are tensions in the left and right hanging part of the string.
Applying Newton’s law of motion,
$\Rightarrow {M_A} \times g - {T_1} = {M_A}a$ ………….. (1)
Where ${M_A}$ is the mass of block A, $g$is the acceleration, ${T_1}$ is the tension of block A and $a$ is the acceleration.
$\Rightarrow {T_2} - {M_B} \times g = {M_B}a$ …………… (2)
Where ${M_B}$ is the mass of block B, $g$is the acceleration, ${T_2}$is the tension of block B and $a$is the acceleration.
$\Rightarrow {T_1}R - {T_2}R = I\dfrac{a}{R}$ ……………. (3)
Where $I$ is the moment of inertia of disc C about its axis.
$I = \dfrac{1}{2}{M_c}{R^2}$
On solving above three equations and substituting given values,
$\Rightarrow 4g - \dfrac{1}{2} \times 40 \times a - 2g = 6a$
$\therefore a = \dfrac{{10}}{{13}}m{s^{ - 2}}$
Angular acceleration of disc, $\alpha = \dfrac{a}{R}$
$ \Rightarrow \alpha = \dfrac{{\dfrac{{10}}{{13}}}}{{0.1}}$
 $\therefore \dfrac{{100}}{{13}}rad{s^{ - 2}}$
On applying Newton motion’s equation,
$ \Rightarrow \theta = {\omega _0}t + \dfrac{1}{2}\alpha {t^2}$
$ \Rightarrow {\omega _0} = 0$
$ \Rightarrow \theta = 0 + \dfrac{1}{2} \times \dfrac{{100}}{{13}} \times {10^2}$
$ \Rightarrow \theta = \dfrac{{5000}}{{13}}rad$
Number of revolutions in $10\operatorname{Sec} $ $ = \dfrac{{\dfrac{{5000}}{{13}}}}{{2\pi }}$
\[\therefore \dfrac{{5000}}{{26\pi }}\]
From equation (1), $4g - {T_1} = 4a$
$\Rightarrow a = \dfrac{{10}}{{13}}rad{s^{ - 2}}$
$\therefore {T_1} = \dfrac{{480}}{{13}}N$

Correct options is (A),(B),(C).

Additional information:
Suppose an object of mass $M$ is suspended by a string from the ceiling. The string is in a state of tension. The molecules of the string near the lower end exert force on the molecule of the object. The resultant of these electromagnetic forces is the force exerted by the string on the object which is called “tension” denoted by $T$. This supports the objects and prevents it from falling. It is directed away from the object. If the string is weightless then the tension in the string is the same at each and every point of the string. If we consider a point A of the string the tension in the part below A and above A are each equal to $T$ and directed away from A. Similarly, the tension at the upper end pulls the ceiling down and the ceiling pulls the string upward. Here also the tension in the string is directed away from the ceiling.

Note:
In this type of question, we should know about the vector. Because here direction upward and downward can be added or subtracted based on vector direction.
Weight is the force with which the object is attracted to the earth.