Question

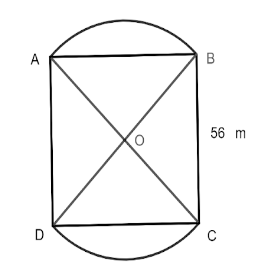
In the fig. Two circular flower beds are shown on the two sides of a square lawn \[ABCD\] on side \[56{\text{ }}m\]. If the centre of the circular flower bed is the point of intersection \[O\] of the diagonal of the square lawn. Find the sum of the area of the lawn and the flower bed.

Answer 1

Hint:In this problem, we have to find the sum of the area of square lawn and the flower beds. We will first find the area of the square lawn. And then we will find the area of the flower bed. We add both the areas to get the desired solution.

Formula used:
We use the formulas are,
Area of square \[ = \]\[{a^2}\] where \[a\] is the side of the square.
Area of semicircle \[ = \]\[\dfrac{1}{2}\pi {r^2}\] where \[r\] is the radius of the circle.

Complete step by step answer:
We are given a diagram represent two circular flower beds are shown on the two sides of a square lawn \[ABCD\] of side \[56{\text{ }}m\]. If the centre of the circular flower bed is the point of intersection \[O\] of the diagonal of the square lawn.

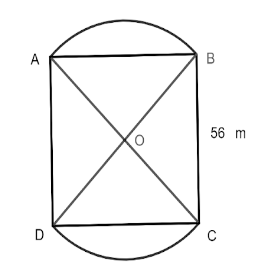
This problem is based on mensuration. Mensuration is the branch of mathematics that deals with measurement or calculation of area, perimeter etc. In order to determine the sum of the area of the lawn and the flower bed. Square is a closed figure bounded by \[4\] equal line segments.

Consider the given question,
Side of square \[ = \]\[56{\text{ }}m\]
Area of square \[ = \]\[56 \times 56 = 3136{\kern 1pt} {\kern 1pt} {\kern 1pt} {m^2}\]
Diagonal of square \[ = \]\[\sqrt 2 a\] . where \[a\] is the side of the square.
Since, The side of square \[ = \]\[56{\text{ }}m\]
Now, we have to radius of the flowerbed, then
Radius of the flowerbed \[ = \] \[\dfrac{1}{2}\] \[ \times \] diagonal of square lawn
Radius of the flowerbed \[ = \dfrac{1}{2} \times \sqrt 2 a = \dfrac{1}{2} \times \sqrt 2 \times 56 = 28\sqrt 2 \\ \]

Therefore, Radius of the flowerbed is \[ = 28\sqrt 2 \].
We can find the total area of the flower bed, then
We know that, the Area of semicircle \[ = \]\[\dfrac{1}{2}\pi {r^2}\]
Total Area of flower bed \[ = \]\[2 \times \dfrac{1}{2}\pi {r^2} = \pi {r^2}\]
Total Area of flower bed \[= \dfrac{{22}}{7} \times 28\sqrt 2 \times 28\sqrt 2 = 4928\; c{m^2}\]
$\text{Total area of given figure=area of square lawn+area of flower bed}$
Total area of given figure \[ = \] \[3136 + 4928 = 8064 \;c{m^2}\]

Hence, the sum of the area of the flower bed and square lawn is \[8064\,c{m^2}\].

Note: We should know the basics of mensuration before attempting such questions. The formulae for areas of circle and square should be remembered thoroughly in order to get to the required answer. Take care of the calculations so as to be sure of the final answer. Always cancel the common factors in numerator and denominator to provide the answer in the simplest form possible.