Question

In the fig $ AX $ and $ CY $ are respectively the bisectors of the opposite angles of $ A $ and $ C $ of a parallelogram $ ABCD $ . Show that $ AX||CY $ .

Answer 1

Hint: As we know that a parallelogram is a type of quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and opposite angles of a parallelogram are of equal measure. There is another property that the diagonals of a parallelogram bisect each other and the diagonal divides the parallelogram into two congruent triangles.

Complete step-by-step answer:
Let us first draw the diagram according to the data given in the question:

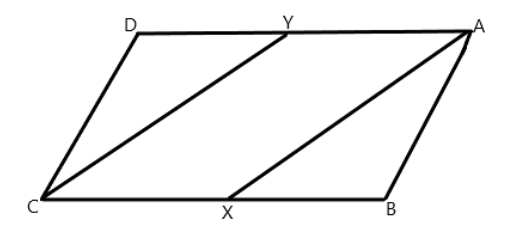
Now by the property of a parallelogram we can say that $ \angle A = \angle C $ ( Opposite angles of a parallelogram are equal).
We will now divide both the sides by $ 2 $ i.e. $ \dfrac{1}{2}\angle A = \dfrac{1}{2}\angle C $ , So it gives us that $ \angle YAX = \angle YCX $ .
If the angles are equal then their halves are also equal.
Also we know that if two lines are parallel then the sum of their adjacent angles is equal to $ {180^ \circ } $ .
So we can write $ \angle AYC + \angle YCX = {180^ \circ } $ , because $ YA||CX $ .
We have solved before that $ \angle YAX = \angle YCX $ , by putting this in the equation we can write that: $ \angle AYC + \angle YAX = 180 $ .
Therefore we can say that $ AX||CY $ because the interior angles on the same side of the transversal are supplementary.
Hence proved that $ AX||CY $ .

Note: Before solving this kind of question we should have the clear concept of parallelograms and their properties. We should note that if any of the angles of a parallelogram is a right angle, then its other angles will also be a right angle. Area of the parallelogram is $ base \times height $ . We know that there are three different types of parallelogram i.e. Square, Rectangle and Rhombus.