Question

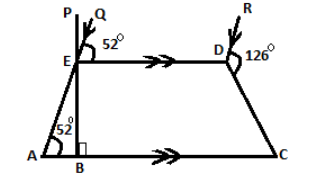
In the diagram,$ACDE$ is a trapezium with $AC\parallel ED$, given that $\angle EAB = {52^\circ}$, $\angle CDR = {126^\circ}$, $\angle PBC = {90^\circ}$and $EQ\parallel DR$. Then $\angle BCD$ equals

A) ${36^\circ}$
B) ${74^\circ}$
C) ${54^\circ}$
D) ${38^\circ}$

Answer 1

Hint:: In this question we have to find out the value of $\angle BCD$. The given figure is a trapezium. A trapezium is a quadrilateral having a pair of sides parallel to each other and other pair may or may not be equal. One should know the property of trapezium and parallel line with a transversal for solving this question. Find out the value of $\angle RDE$ and then find out $\angle EDC$ and at last work out the value of $\angle DCA$.

Complete step by step solution:
In the given trapezium $ACDE$,
$QE\parallel RD$are parallel and $ED$is a transversal.
We know,
If $QE\parallel RD$are parallel and $ED$is transversal, then,
Sum of integer angles are supplementary i.e. ${180^\circ}$
$\therefore \angle QED + \angle RDE = {180^\circ}$ $\left[ {\angle QED = {{52}^\circ},given} \right].$
$\therefore {52^\circ} + \angle RDE = {180^\circ}$
$ \Rightarrow \angle RDE = {128^\circ}$
From the figure –
$\angle RDE + \angle RDC + \angle EDC = {360^\circ}$as it makes a complete circle.
$ \Rightarrow {128^\circ} + {126^\circ} + \angle EDC = {360^\circ}$ $\left[ {\because \angle RDC = {{126}^\circ}} \right]$
$ \angle EDC = {360^\circ} - {128^\circ} - {126^\circ} = {360^\circ} - {254^\circ} = {106^\circ}$
Again, in trapezium $ACDE$ –
$ED\parallel AB$.
$\therefore \angle EDC$and $\angle DCB$are interior angles.
$
 \angle EDC + \angle DCB = {180^\circ} \\
  {106^\circ} + \angle DCB = {180^\circ} \\
   \Rightarrow \angle DCB = {180^\circ} - {106^\circ} = {74^\circ} \\
 $

$\therefore$The $\angle BCD$ is ${74^\circ}$. Correct option is (B).

Note: The asked question was from the geometric portion so we need to have knowledge about the properties of the trapezium. In these types of questions the diagram should be clear. Read the question very carefully relating the given information to the diagram & to understand what answer they have asked for. Different rules of geometry about supplementary angles, the sum of all angles around a point is $360^\circ $should always be kept in mind while doing geometry problems otherwise you won’t be able to establish a relationship between different angles. Make sure that you don’t make a mistake in the calculation because that will bring an incorrect answer instead of having all the concepts & procedures clear in your mind.