Question

In the diagram \[\overrightarrow {OA} = a\] and \[\overrightarrow {OB} = b\].
a. Find in terms of \[a\] and \[b\]:
i. \[\overrightarrow {OC} \]
ii. \[\overrightarrow {OE} \]
iii. \[\overrightarrow {OD} \]
iv. \[\overrightarrow {DC} \]
v. \[\overrightarrow {DE} \]
b. If\[\left| a \right| = 1\] and \[\left| b \right| = 2\],
find:
i. \[\left| {\overrightarrow {OC} } \right|\]
ii. \[\left| {\overrightarrow {OE} } \right|\]
iii. \[\left| {\overrightarrow {OD} } \right|\]

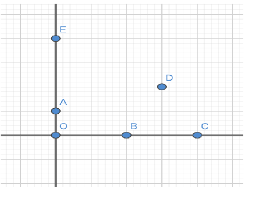
Answer 1

Hint: This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. To solve this question we need to know how to compare one vector value with another vector value. We need to know how to find the magnitude of the particular vector. Also, we need to know the formula for finding a magnitude of a vector. Also, we need to know the Pythagoras theorem to solve this question.

Complete step by step solution:
In the given question we have

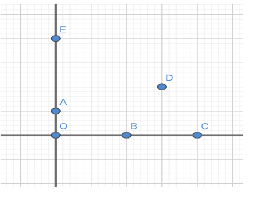
(Here \[\overrightarrow {OA} = a\] and \[\overrightarrow {OB} = b\])
Let’s solve the case: a
i. \[\overrightarrow {OC} \]
We know that\[\overrightarrow {OB} = b\].
From the figure we get\[\overrightarrow {BC} = \overrightarrow {OB} \]
So, we get
\[
\overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {BC} \\
\overrightarrow {OC} = b + b \\
\overrightarrow {OC} = 2b \\
\] (Here the value of\[\overrightarrow {OC} \] is two times of \[\overrightarrow {OB} \])
ii. \[\overrightarrow {OE} \]
We know that\[\overrightarrow {OA} = a\].
From the figure we get
\[
\overrightarrow {OE} = 4 \times \overrightarrow {OA} \\
\overrightarrow {OE} = 4 \times a \\
\overrightarrow {OE} = 4a \\
\] (Here the value of\[\overrightarrow {OE} \] is four times of \[\overrightarrow {OA} \])
iii. \[\overrightarrow {OD} \]
Let’ see the given figure below,

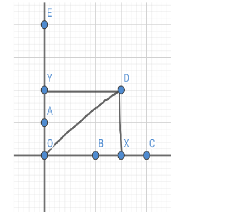
(Here we mark the points \[X\] and \[Y\] in the above figure to make easy calculation)
From the above figure we get,
\[O{D^2} = O{X^2} + X{D^2}\] (By using Pythagoras theorem in a triangle \[ODX\])
Here, \[OX = OB + \dfrac{{BC}}{2}\] (Here \[\dfrac{{BC}}{2}\] can also be expressed as \[BX\])
We know that,
\[
OB = b \\
\dfrac{{BC}}{2} = \dfrac{b}{2} \\
\]
So, we can write
\[O{X^2} = {\left( {b + \dfrac{b}{2}} \right)^2}\]
(Let’s convert the mixed fraction term into simple fraction term)
\[
O{X^2} = {\left( {\dfrac{{2b + b}}{2}} \right)^2} = {\left( {\dfrac{{3b}}{2}} \right)^2} \\
O{X^2} = \dfrac{{9{b^2}}}{4} \\
\] (Here we use the formula\[{\left( {\dfrac{a}{b}} \right)^m} = \dfrac{{{a^m}}}{{{b^m}}}\])
We know that,
\[
XD = OY \\
OY = OA + AY = a + a = 2a \\
O{Y^2} = X{D^2} = 4{a^2} \\
\] (Here \[OY\] is equal to two times of \[OA\])
So, we get
\[O{D^2} = O{X^2} + X{D^2}\] (By using Pythagoras theorem in the triangle \[ODX\])
\[O{D^2} = \dfrac{{9{b^2}}}{4} + 4{a^2}\]
\[\overrightarrow {OD} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \]
iv. \[\overrightarrow {DC} \]
To solve the above-mentioned term the following figure will help us,

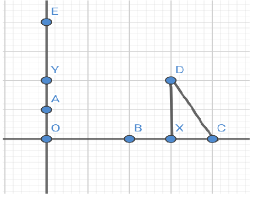
So, we get
\[D{C^2} = X{D^2} + X{C^2}\]
We know that,
\[X{D^2} = 4{a^2}\] (This equation is already solved in the above steps)
\[X{C^2} = {\left( {\dfrac{b}{2}} \right)^2} = \dfrac{{{b^2}}}{4}\] (Here we use the
formula\[{\left( {\dfrac{a}{b}} \right)^m} = \dfrac{{{a^m}}}{{{b^m}}}\])
We get, \[D{C^2} = X{D^2} + X{C^2}\]
\[
D{C^2} = 4{a^2} + \dfrac{{{b^2}}}{4} \\
\overrightarrow {DC} = \sqrt {4{a^2} + \dfrac{{{b^2}}}{4}} \\
\] (Here we take square root on both sides of the equation)
v. \[\overrightarrow {DE} \]
From the figure we get,
\[\overrightarrow {DE} = \overrightarrow {OD} \]
\[\overrightarrow {DE} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \] (The value of \[\overrightarrow
{OD} \] is already solved in the above steps)

Let’s solve the case: b
Here, \[\left| a \right| = 1\] and \[\left| b \right| = 2\]
i. \[\left| {\overrightarrow {OC} } \right|\]
We know that,
\[
\overrightarrow {OC} = 2b \\
\left| {\overrightarrow {OC} } \right| = 2\left| b \right| = 2 \times 2 = 4 \\
\] (Here we substitute\[\left| b \right| = 2\])
ii. \[\left| {\overrightarrow {OE} } \right|\]
We know that,
\[
\overrightarrow {OE} = 4a \\
\left| {\overrightarrow {OE} } \right| = 4\left| a \right| = 4 \times 1 = 4 \\
\] (Here we substitute\[\left| a \right| = 1\])
iii. \[\left| {\overrightarrow {OD} } \right|\]
We know that,
\[\overrightarrow {OD} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \]
\[\left| {\overrightarrow {OD} } \right| = \sqrt {\dfrac{{9\left| {{b^2}} \right|}}{4} + 4\left|
{{a^2}} \right|} \] (Here we take determinant on both sides of the equation)
\[\left| {\overrightarrow {OD} } \right| = \sqrt {\dfrac{{9 \times {2^2}}}{4} + 4 \times {1^2}} \]
(Here, we substitute\[\left| a \right| = 1\] and \[\left| b \right| = 2\])
\[\left| {\overrightarrow {OD} } \right| = \sqrt {\dfrac{{9 \times 4}}{4} + 4} \] (We know
that\[{2^2} = 4and{1^2} = 1\])
\[\left| {\overrightarrow {OD} } \right| = \sqrt {9 + 4} \] (Here \[4\] in the numerator and \[4\] in the denominator can be cancelled each other)
\[\left| {\overrightarrow {OD} } \right| = \sqrt {13} \]

So, the final answer is,
\[
\overrightarrow {OC} = 2b \\
\overrightarrow {OE} = 4a \\
\overrightarrow {OD} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \\
\overrightarrow {DC} = \sqrt {4{a^2} + \dfrac{{{b^2}}}{4}} \\
\overrightarrow {DE} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \\
\left| {\overrightarrow {OC} } \right| = 4 \\
\left| {\overrightarrow {OE} } \right| = 4 \\
\left| {\overrightarrow {OD} } \right| = \sqrt {13} \\
\\
\\
\]

Note: This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. Remember the Pythagoras theorem to solve this type of question. Also, we would compare the unknown vector with the known vector to find the solution. Remember the process to find the magnitude of a vector.