Question

In the diagram, \[CB\] and \[CD\] are tangents to the circle with centre \[O\] . \[AOC\] is a straight line and \[\angle OCB = {34^ \circ }.\angle ABO\] equals.

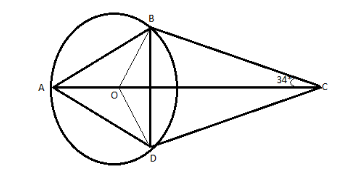
A. \[{56^ \circ }\]
B. \[{28^ \circ }\]
C. \[{34^ \circ }\]
D. \[{32^ \circ }\]

Answer 1

Hint: In this problem, we need to find the tangent of a circle with the given geometric representation line that touches the circle at a single point is known as a tangent to a circle. The point where tangent meets the circle is called the point of tangency.

Complete step-by-step answer:
In the given problem,
\[CB\] and \[CD\] are tangents to the circle with centre \[O\] .
\[AOC\] is a straight line and \[\angle OCB = {34^ \circ }.\angle ABO\] equals.
In \[\Delta AOB\] (Isosceles triangle property)
 \[OA = OB\] (radius of the circle)
Here, a triangle whose two sides are equal and one side are unequal.
Therefore, \[\angle OBA = \angle OAB = x\] (Isosceles triangle property)
Then, the angle between the radius of the tangent
Also, \[\angle OBC = {90^ \circ }\]
Now,In \[\Delta AOC\] (Isosceles triangle property)
Sum of the property of the triangle is equal to \[{180^ \circ }\] .
 \[\angle ACB + \angle BAC + \angle ABC = {180^ \circ }\]
According to the isosceles triangle whose two equal sides,one side is unequal.
 \[2x + {90^ \circ } + {34^ \circ } = {180^ \circ }\]
By simplify it, we get
 \[2x + {124^ \circ } = {180^ \circ }\]
Now, we get
 \[
  2x = {180^ \circ } - {124^ \circ } \\
  x = \dfrac{{{{56}^ \circ }}}{2} = {28^ \circ } \\
\]
Hence, the isosceles triangle, \[\angle ABO = {28^ \circ }\]
The final answer is option(B) \[{28^ \circ }\]
So, the correct answer is “Option B”.

Note: In this question, tangent of the circle and isosceles triangle property are used to find the solution with respect to the problem.here, the tangent to a circle is defined as a straight line that touches the circle at a single point.The point where the tangent touches a circle and also isosceles triangle is the concept of two sides are equal and one unequal sides. These are the concepts used for finding the tangent of the circle.