Question

In the complex plane, let ${z_1} = \sqrt 3 + i\;and\;{z_2} = \sqrt 3 - i$ be two adjacent vertices of n sided regular polygon centered at the origin. The n equals
A.4
B.6
C.8
D.12

Answer 1

Hint: Draw the given points in a complex plane, then figure out the angle subtended by them on the center or the origin then add angles subtended by both points to get the angle subtended by the side of the regular polygon and use the property of the polygon that sum of angles subtended by each side of the polygon equals ${360^0}$ and accordingly find the number of side.

Complete step by step solution:
In order to find the number of sides of the regular polygon whose adjacent sides are ${z_1} = \sqrt 3 + i\;and\;{z_2} = \sqrt 3 - i$, we will first draw them on a complex plane to clarify the image more

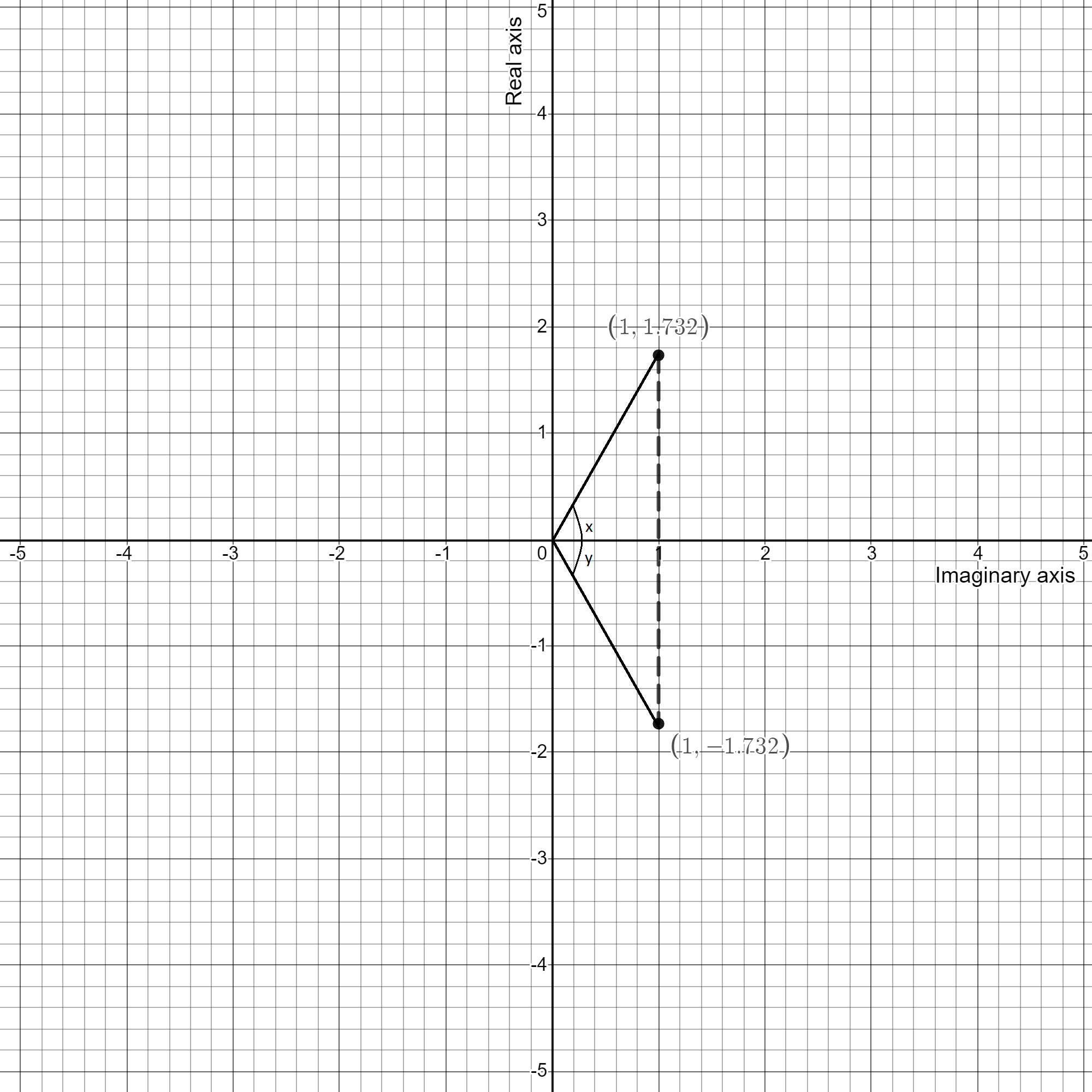
Here we can see that ${z_1} = \sqrt 3 + i\;and\;{z_2} = \sqrt 3 - i$ are subtending angles $x\;{\text{and}}\;y$ at the origin and also we can say that $x = y$, we can find their values as follows
$x = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) = {30^0}$
Therefore whole angle subtended by the given side will be $ = x + y = {30^0} + {30^0} = {60^0}$
Now we know that sum of the angles subtended by all sides at origin is equals to ${360^0}$, also in question it is given that this is a regular polygon, therefore contribution in angle ${360^0}$ is equal for each sides, so if there are n sides in the polygon, then we can write that
$
   \Rightarrow {60^0} \times n = {360^0} \\
   \Rightarrow n = \dfrac{{{{360}^0}}}{{{{60}^0}}} = 6 \\
 $
Therefore this is a six sided polygon.

Note:
This question can be solved directly by finding the argument of the complex points about the origin and then add the arguments of complex points to get the angle subtended by the side to the origin and complete further as we have proceeded above.