Question

In the circuit shown $ {V_{AB}} = {V_{BC}} $ . Then $ X $ is combination of:

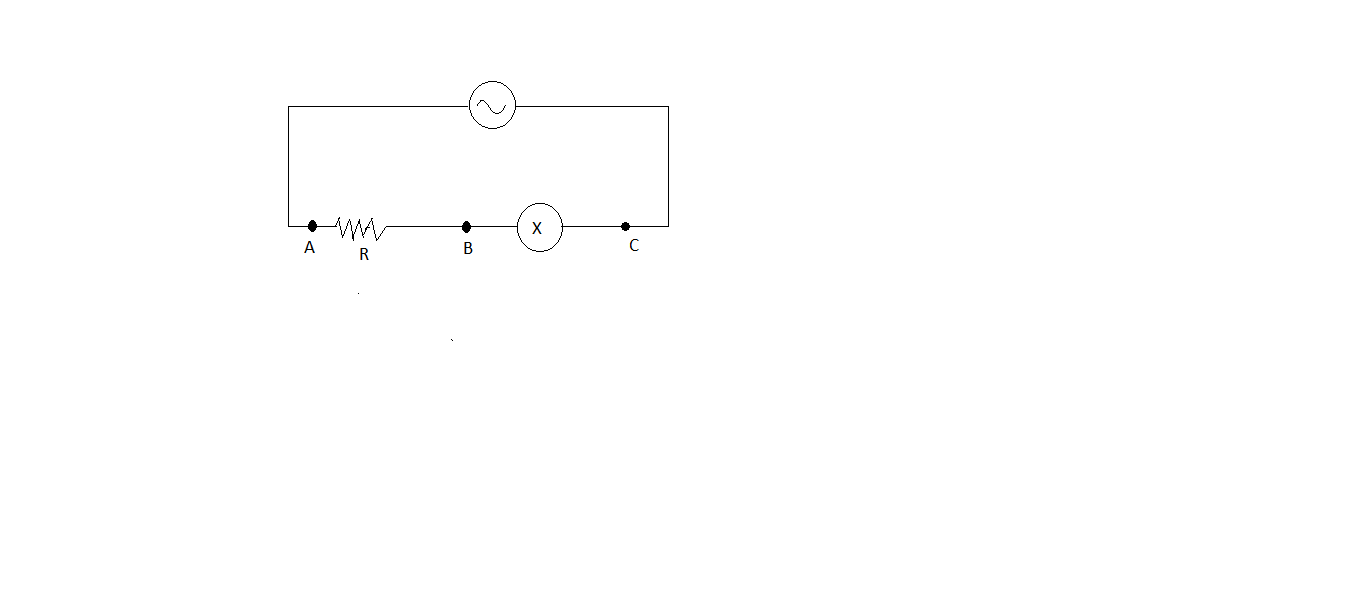
 $ \left( A \right)\;\;inductors{\text{ }}in{\text{ }}parallel \\
  \left( B \right)\;\;a{\text{ }}capacitor{\text{ }}and{\text{ }}a{\text{ }}resistor \\
  \left( C \right)\;\;an{\text{ }}inductor{\text{ }}and{\text{ }}a{\text{ }}capacitor \\
  \left( D \right)\;\;an{\text{ }}inductor{\text{ }}and{\text{ }}a{\text{ }}resistor \\ $

Answer 1

Hint :In the circuit shown, it is given that the voltages across the two elements is same
 $ {V_{AB}} = {V_{BC}} $ , If we analyze all the options one by one, then we can get a solution based on what the resultant voltages for each element are going to be if connected with the resistor.
For an $ RL $ circuit, the expression for the voltage $ {V_G} $ is
 $ {V_G} = \sqrt {{V_R}^2 + {V_L}^2} $
While for $ RC $ circuit,
 $ {V_G} = \sqrt {{V_R}^2 + {V_C}^2} $

Complete Step By Step Answer:
Case 1: $ X $ is a combination of inductors in parallel
This will give a sub element with a number of parallel inductors having same voltages, thus, $ AC $ will be a series combination of a resistor and an inductor which doesn’t mean that the two elements are going to have equal voltages.
Case $ 2 $ : $ X $ is a combination of a capacitor and a resistor
For an $ RL $ circuit, the resulting voltage lies in a direction with an angle to the direction of R
As we can see in the figure and the expression for the voltage $ {V_G} $ is
 $ {V_G} = \sqrt {{V_R}^2 + {V_L}^2} $
Case $ 3 $ : If $ X $ is a combination of an inductor and a capacitor, the voltages $ {V_L} $ and $ {V_C} $ will be equal and opposite thus resulting in a zero net voltage, which will not be equal to $ {V_R} $
Case $ 4 $ : If $ X $ is a combination of an inductor and a resistor, the resulting net voltage will be equal to
 $ {V_G} = \sqrt {{V_R}^2 + {V_C}^2} $ and in a direction at an angle $ \theta $ to the direction of the resistor voltage.
Here, the two cases are possible, if $ X $ is a combination of a capacitor and a resistor or an inductor and a resistor. Hence, option (B) and (D) are correct.

Note :
The values of the resistor and the capacitor as well as that for the resistor and the inductor are so chosen that the angle is such that the resulting voltage lies in the direction of resistance only, in such a case, the value of the voltage will be same as that for the resistance i.e. the condition $ {V_{AB}} = {V_{BC}} $ is fulfilled.