Question

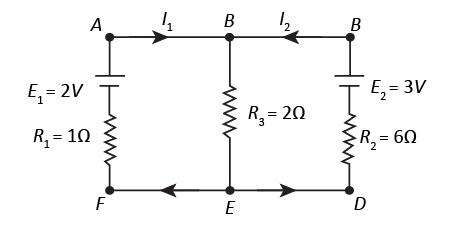
In the circuit shown in Figure above, ${E_1}$ and ${E_2}$ are two cells having emfs $2\;{\rm{V}}$ and $3\;{\rm{V}}$ respectively, and negligible internal resistances. Applying Kirchhoff’s laws of electrical networks, find the values of currents ${I_1}$ and ${I_2}$.

Answer 1

Hint: We should apply Kirchhoff’s second law in this question. Apply the second law in both the meshes of the given circuit and obtain algebraic equations. We just have to solve the equations to obtain the values of currents.

Complete step by step answer:
Given: Emf of the first cell, ${E_1} = 2\;{\rm{V}}$, Emf of the second cell, ${E_2} = 3\;{\rm{V}}$
We have to apply Kirchhoff’s laws to find the values of currents flowing through different segments of the circuit.According to Kirchhoff’s second law, the algebraic sum of all the voltage in a closed loop of a circuit is equal to zero. So, let us apply Kirchhoff’s second law to the mesh $ABEF$. Applying the law, we get,
${R_3}\left( {{I_1} + {I_2}} \right) + {R_1}{I_1} - {E_1} = 0$

Now, since ${R_1} = 1\;\Omega $, ${R_3} = 2\;\Omega $ and ${E_1} = 2\;{\rm{V}}$, we can substitute the values for ${R_1}$, ${R_3}$ and ${E_1}$ in the above equation to get,
$
2\left( {{I_1} + {I_2}} \right) + 1 \times {I_1} - 2 = 0\\
\Rightarrow 2{I_1} + 2{I_2} + {I_1} = 2\\
\Rightarrow 3{I_1} + 2{I_2} = 2$
Now, let us apply Kirchhoff’s second law to the mesh $BCDE$. Applying the law, we get
${R_3}\left( {{I_1} + {I_2}} \right) + {R_2}{I_2} - {E_2} = 0$
It is given in the diagram that ${R_2} = 6\;\Omega $. So, substituting the values for ${R_{_2}}$, ${R_3}$ and ${E_2}$ in the above equation we get,
$2\left( {{I_1} + {I_2}} \right) + 6{I_2} - 3 = 0\\
\Rightarrow 2{I_1} + 2{I_2} + 6{I_2} = 3\\
\Rightarrow 2{I_1} + 8{I_2} = 3$

Now, consider the two equations we obtained.
$3{I_1} + 2{I_2} = 2$ ……………(1)
$2{I_1} + 8{I_2} = 3$ ………….(2)
Now, let’s multiply equation (1) by $4$. Then, we get
$12{I_1} + 8{I_2} = 8$ ……..(3)
Now we subtract equation (2) from equation (3). Then, we get
$12{I_1} + 8{I_2} - \left( {2{I_1} + 8{I_2}} \right) = 8 - 3\\
\Rightarrow 10{I_1} = 5\\
\Rightarrow {I_1} = \dfrac{5}{{10}}\\
\Rightarrow \dfrac{1}{2}\;{\rm{A}}$

Now, we can substitute the value of ${I_1}$ in the equation $3{I_1} + 2{I_2} = 2$ to get the value of ${I_2}$.
$3 \times \dfrac{1}{2} + 2{I_2} = 2\\
\Rightarrow 2{I_2} = 2 - \dfrac{3}{2}\\
\Rightarrow 2{I_2} = \dfrac{{4 - 3}}{2}\\
\Rightarrow {I_2} = \dfrac{1}{4}\;{\rm{A}}$

Hence, the values of currents${I_1}$ and ${I_2}$ are obtained as $\dfrac{1}{2}\;{\rm{A}}$ and $\dfrac{1}{4}\;{\rm{A}}$ respectively.

Note:We should be careful in putting proper signs to the algebraic terms so that we get the correct answer. If we take the clockwise current as positive, then all the currents in the anticlockwise direction should be taken as negative while taking the algebraic sum.