Question

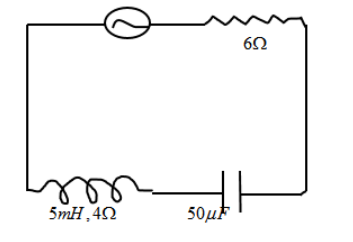
In the circuit shown below, the ac source has voltage \[V = 20\cos (\omega t)volt\] with \[\omega = 2000rad/s\] The amplitude of the current will be nearest to-

(a) \[2A\]
(b) \[3.3A\]
(c) \[2/\sqrt 5 A\]
(d) \[\sqrt 5 A\]

Answer 1

Hint: Its LCR ac circuit draw phase diagram to find the phase difference between current and voltage and then calculate the impedance of the circuit once you know the impedance then take the ratio of voltage and impedance and adjust the phase difference you will get the expression and its asking the amplitude of the current which is maximum value of the current in an AC circuit.

Complete step by step answer:
Here we will calculate the impedance of the circuit by calculating resistance, capacitive reactance and inductive reactance then adding to get total impedance
Resistance of the circuit \[R = 6\Omega + 4\Omega = 10\Omega \]
Capacitive reactance \[\]\[{X_c} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2000 \times 50 \times {{10}^{ - 6}}}} = 10\] and,
Inductive reactance \[{X_L} = \omega L = 2000 \times 5 \times {10^{ - 3}} = 10\]
Here \[{X_L}\] and \[{X_C}\] are same it means the circuit is in resonance so there will be no phase difference between current and voltage
So total reactance or impedance \[Z = \sqrt {{{({X_C} - {X_L})}^2} + {R^2}} = 10\]
We know that current in an ac circuit \[I = \dfrac{V}{Z}\]
Therefore \[I = \dfrac{{20\cos (\omega t)}}{{10}} = 2\cos (\omega t)\]ampere
Now amplitude of current is the maximum value of current and as we can we see from the expression of current it is 2A.

Hence, Option (A) is correct.

Note: As its an LCR circuit you have to keep in mind that first you need to find impedance then you will get the expression of current by taking ratio of voltage and impedance and taking care of phase difference between once you know the expression for the current it's easy to find the amplitude of the current.