Question

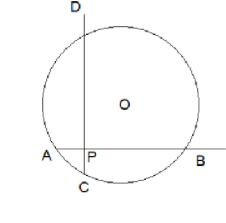
In the circle with center O as shown chord AB and CD intersect at P and are perpendicular to each other.
If AP \[=4cm\], PB \[=6cm\] and PC \[=2cm\], then the area of the circle is

Answer 1

Hint:First we need to find the length of the chord DP and after that we need to extend a line from O to A and another from O to midpoint of the chord CD and then form a four sided figure with OMPN, N being a point on AB and then with the help of the four sided figure we find the value of the radius in form of OA and with it we find the area of the circle.

Complete step by step solution:
As given in the question, and the diagram drawn below, we can say that the value of CM and AN as:

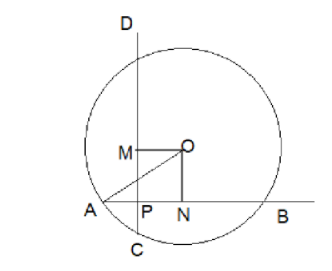
CM \[=\dfrac{1}{2}\] CD and AN \[=\dfrac{1}{2}\] BD
As both the above values are perpendicular to the center of the circle given which bisects the circle using the chord CD and AB

Now, the total length of the chord AB can be written as AB = AP \[+\ PB \=\left( 4+6 \right)cm=10cm\].

With the two chords intersecting at point P, the relationship between the parts of each chord is written as PD \[=\dfrac{\text{AP}\times \text{BP}}{\text{PC}}\]

Placing the values in the formula we get the value of PD as:
\[\Rightarrow \dfrac{4\times 6}{2}\]
\[\Rightarrow 12cm\]
The value of the chord CD with the help of PD is written as:
\[\Rightarrow \] CD = PD \[+\] PC
\[\Rightarrow \left( 12+2 \right)=14cm\]
Therefore, the value of CM is given as \[\dfrac{1}{2}\times 14cm=7cm\] and AN as \[\dfrac{1}{2}\times
10cm=5cm\].

Hence, we have the value of CM and PC, so the value of PM is equal to CM \[-\] PC which is:
\[\Rightarrow 7-2=5cm\].
As the two chords are at perpendicular to each other as given in the question, the figure PNOM is a rectangle as the line OM is drawn straight from the middle of the chord to the center point of the circle with the value of:
ON = PM = \[5cm\].

With the values of ON and AN known we can find the value of AO which will give us the radius of the circle and then finally the area of the circle. The length of the hypotenuse of the triangle NOA is:

\[\Rightarrow OA=\sqrt{O{{N}^{2}}+A{{N}^{2}}}\]
\[\Rightarrow OA=\sqrt{{{5}^{2}}+{{5}^{2}}}\]
\[\Rightarrow OA=\sqrt{50}\]

Now using the formula for the area of the circle as \[\pi {{r}^{2}}\] where \[r=\] OA, we get the area of the circle as:

\[\Rightarrow \pi {{r}^{2}}\]
\[\Rightarrow \pi \times {{\sqrt{50}}^{2}}\]
\[\Rightarrow 50\pi \text{ }c{{m}^{2}}\]

Note:Student may go wrong if they try to think the point O is midpoint for the points D and B as in some place it might be accurate by here we don’t know, if the procedure will follow therefore, it is wise to first solve for the chord or line whose measurement are not given and then make a small rectangle like figure with the help of those chord to find the length of the radius of the triangle.