Question

In the circle, AB is a diameter, chord AD = DC and $ \angle ABC={{50}^{0}} $ . Find $ \angle CBD $ and $ \angle DAB $ .

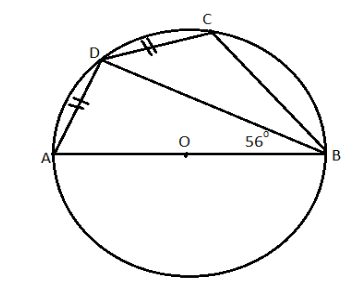
Answer 1

Hint: Here, we will use the property that the sum of the opposite angles of a cyclic quadrilateral is $ {{180}^{0}} $ . We will also use the property of a triangle that the sum of all angles of a triangle is $ {{180}^{0}} $ and also that the angle in a semicircle is equal to $ {{90}^{0}} $ .

Complete step-by-step answer:

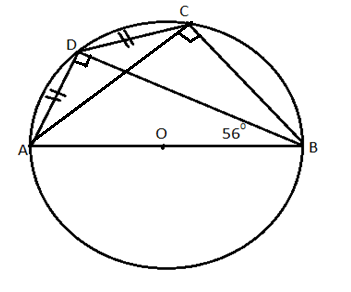
Now, since we know that the angle in a semicircle is $ {{90}^{0}} $ . So, we can write:
 $ \angle ACB={{90}^{0}} $ and $ \angle ADB={{90}^{0}} $ .
Now, in the triangle ABC, by the angle sum property of a triangle we can write:
 $ \angle ACB+\angle ABC+\angle CAB={{180}^{0}} $
Since, we have $ \angle ABC={{56}^{0}} $ and \[\angle ACB={{90}^{0}}\]. So, on putting these values in the above equation we get:
 $ {{90}^{0}}+{{56}^{0}}+\angle CAB={{180}^{0}} $
 $ \Rightarrow \angle CAB={{180}^{0}}-\left( {{90}^{0}}+{{56}^{0}} \right)={{34}^{0}} $
As ABCD is a cyclic quadrilateral, so the sum of opposite angles is $ {{180}^{0}} $ .
Therefore, $ \angle ABC+\angle ADC={{180}^{0}} $
 $ \Rightarrow \angle ADC={{180}^{0}}-{{56}^{0}}={{124}^{0}} $
We know that the angle in a semicircle is $ {{90}^{0}} $ .
So, $ \angle BDA={{90}^{0}} $
Since, $ \angle ADC={{124}^{0}} $
 $ \begin{align}
  & \Rightarrow \angle BDA+\angle BDC=\angle ADC={{124}^{0}} \\
 & \Rightarrow {{90}^{0}}+\angle BDC={{124}^{0}} \\
 & \Rightarrow \angle BDC={{124}^{0}}-{{90}^{0}}={{34}^{0}} \\
\end{align} $
Now, again in triangle ADC, by the angle sum property we can write:
 $ \angle ADC+\angle DAC+\angle DCA={{180}^{0}} $
Since, angles opposite to equal sides are equal and AD is equal to DC, thus $ \angle DAC=\angle DCA $
 $ \Rightarrow \angle ADC+2\angle DCA={{180}^{0}} $
 $ \begin{align}
  & \Rightarrow {{124}^{0}}+2\angle DCA={{180}^{0}} \\
 & \Rightarrow 2\angle DCA={{180}^{0}}-{{124}^{0}} \\
 & \Rightarrow \angle DCA=\dfrac{{{56}^{0}}}{2}={{28}^{0}} \\
\end{align} $
In triangle BDC:
\[\begin{align}
  & \angle BCD+\angle CDB+\angle CBD={{180}^{0}} \\
 & \Rightarrow \left( \angle ACB+\angle ACD \right)+\left( \angle ADC-\angle ADB \right)+\angle CBD={{180}^{0}} \\
 & \Rightarrow \left( {{90}^{o}}+{{28}^{0}} \right)+\left( {{124}^{0}}-{{90}^{0}} \right)+\angle CBD={{180}^{0}} \\
 & \Rightarrow {{118}^{0}}+{{34}^{0}}+\angle CBD={{180}^{0}} \\
 & \Rightarrow \angle CBD={{180}^{0}}-\left( {{118}^{0}}+{{34}^{0}} \right)={{28}^{0}} \\
\end{align}\]
Now, we have:
 $ \angle DAB=\angle DAC+\angle CAB=\angle DCA+\angle CAB={{28}^{0}}+{{34}^{0}}={{62}^{0}} $
Hence, the values of $ \angle CBD $ and $ \angle DAB $ are $ {{28}^{0}} $ and $ {{62}^{0}} $ .

Note: Students should note remember all the required properties like angle sum property of triangle and the property that the sum of opposite angles of a cyclic quadrilateral is 180 degrees. A possibility of mistake here is that students may start applying different properties to the triangles ABD and CBD that are already given but we also have to do our calculations on the triangle ADC. That is why we need to join A and C and then do the calculations.