Question

In the case of minimum deviation position the, a ray travels within the prism:
a. Symmetrically
b. Asymmetrically
c. Normally
d. Transversally

Answer 1

Hint: We can compare the incidence angle and the emergence angle. With the help of these two values we are able to find the answer to the given question.
Formula used:
$i = e$
Where $i$ is the angle of incidence and $e$ is the angle of emergence.

Complete step by step answer:
To answer the given question, first we need to understand the basic angles of the prism.
Consider a prism. We know that a prism has angles. When a ray that is incident on a surface of a prism is known as Incident ray. The angle between that incident ray and the line that is normal to that particular surface is known as Angle of Incidence.

A ray of light that is bent at a particular point of the prism is known as the Angle of Deviation. Always remember that the angle of deviation decreases with the increase in the angle of incidence. This angle of incidence in a prism where the angle of the deviation is minimum is called the Angle of Minimum Deviation.
The angle of the light that comes out through the medium of the prism is known as the Emergence angle.

Consider the minimum deviation position of the prism. When the angle of the incidence at one surface of the prism and the angle of emergence angle at another surface of the prism, the light rays inside the prism travel parallel to the base. In other words, we can say that the light rays will move symmetrically inside the prism.

The angle of incidence and the angle of emergence are always equal. We can represent this relation mathematically as,
$ \Rightarrow i = e$
Where $i$ is the angle of incidence and $e$ is the angle of emergence

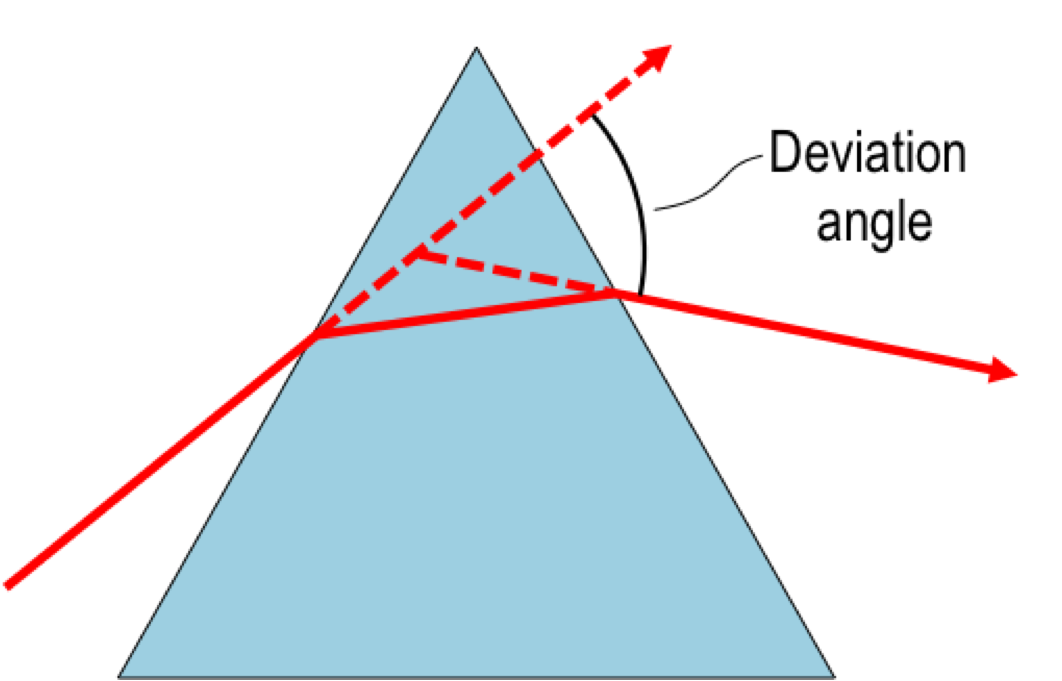
Consider the given diagram of the prism. From the diagram it is clear that the light ray that travels inside the prism is symmetrical to the base.
Therefore, in the case of the minimum deviation position the ray travels symmetrically within the prism.

Hence, the correct answer is option (A).

Note: The formula for the minimum deviation can be derived by changing some terms in the Snell’s law. Mathematically it can be represented as,
$ \Rightarrow n = \dfrac{{\sin \left( {\dfrac{{A + {D_m}}}{2}} \right)}}{{\sin \left( {\dfrac{A}{2}} \right)}}$
Where $A$ is the angle of prism and ${D_m}$ is the angle of minimum deviation.