Question

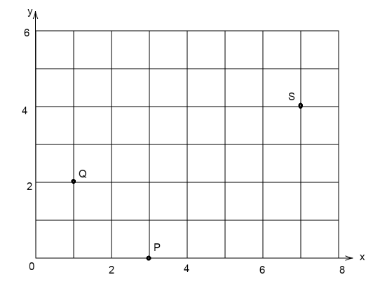
In the Cartesian plane above, the points P, Q and S are three vertices of the rectangle PQRS. Find the coordinates of R.

A. \[(5,6)\]
B. \[(8,2)\]
C. \[(4,6)\]
D. \[(6,4)\]

Answer 1

Hint: We use the general definition of a point in the Cartesian plane and find the distances of the respective points from the origin on y-axis and x-axis. After writing the coordinates of each point we calculate midpoint of diagonals using the formula of midpoint of two points. Equate the values obtained from mid-point using both diagonals.
* Any point on the Cartesian plane is called Cartesian coordinate and is written as \[(a,b)\] where a is the distance of point from origin on x-axis and b is the distance of point from origin on y-axis.
* Midpoint of two points \[(x,y)\] and \[(a,b)\] is given by \[\left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right)\]

Complete step-by-step solution:
We are given the graph having three coordinates of a rectangle PQRS.

We first find the coordinates of points P, Q and S.
Point P:
Distance of point P from origin on x-axis is 3
Distance of point P from origin on y-axis is 0
Point becomes \[P(3,0)\]
Point Q:
Distance of point Q from origin on x-axis is 1
Distance of point Q from origin on y-axis is 2
Point becomes \[Q(1,2)\]
Point S:
Distance of point S from origin on x-axis is 7
Distance of point S from origin on y-axis is 4
Point becomes \[S(7,4)\]
Join the points P and Q to form side PQ and join the points P and S to form side PS of the rectangle PQRS. Let the fourth vertex of the rectangle be R having coordinates \[(x,y)\]. Join all sides of the rectangle and form diagonals PR and QS bisecting each other at point O.
Since we know diagonals of a rectangle bisect each other, that means the point of intersection of midpoints is the midpoint of the diagonals.

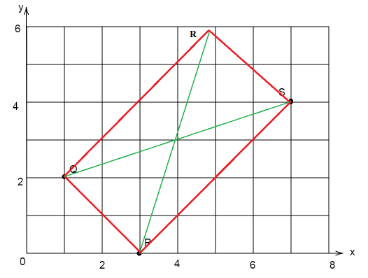
Let the midpoint of the diagonals PR and QS be O.
Use the formula of the midpoint of two points to write the value of O from both diagonals. Midpoint of two points \[(x,y)\] and \[(a,b)\] is given by \[\left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right)\]
Then the value of mid-point from diagonals PR and QS will be the same, as the point O is the mid-point of both diagonals.
\[ \Rightarrow \]Midpoint of PR \[ = \]Midpoint of QS
\[ \Rightarrow \left( {\dfrac{{x + 3}}{2},\dfrac{{0 + y}}{2}} \right) = \left( {\dfrac{{7 + 1}}{2},\dfrac{{4 + 2}}{2}} \right)\]
Calculate the values in RHS
\[ \Rightarrow \left( {\dfrac{{x + 3}}{2},\dfrac{{0 + y}}{2}} \right) = \left( {\dfrac{8}{2},\dfrac{6}{2}} \right)\]
\[ \Rightarrow \left( {\dfrac{{x + 3}}{2},\dfrac{{0 + y}}{2}} \right) = \left( {4,3} \right)\]
Equate the x-coordinate in LHS to x-coordinate in RHS and y-coordinate in LHS to y-coordinate in RHS.
\[ \Rightarrow \dfrac{{x + 3}}{2} = 4\] and \[\dfrac{y}{2} = 3\]
Cross multiply the values
\[ \Rightarrow x + 3 = 8\] and \[y = 6\]
Shift constant values to RHS
\[ \Rightarrow x = 8 - 3\] and \[y = 6\]
\[ \Rightarrow x = 5\] and \[y = 6\]
So, the point R becomes \[(5,6)\]
\[\therefore \]Coordinates of point R are \[(5,6)\]

\[\therefore \]Option A is correct.

Note: Many students make mistake of solving for the coordinates of R using the distance formula between two points which is wrong as then we will have two quadratic equations in two variables and we don’t know how to solve them, So we use the fact that the figure is given as rectangle.
In a rectangle the opposite sides are equal. All the internal angles are equal to $90^\circ$.