Question

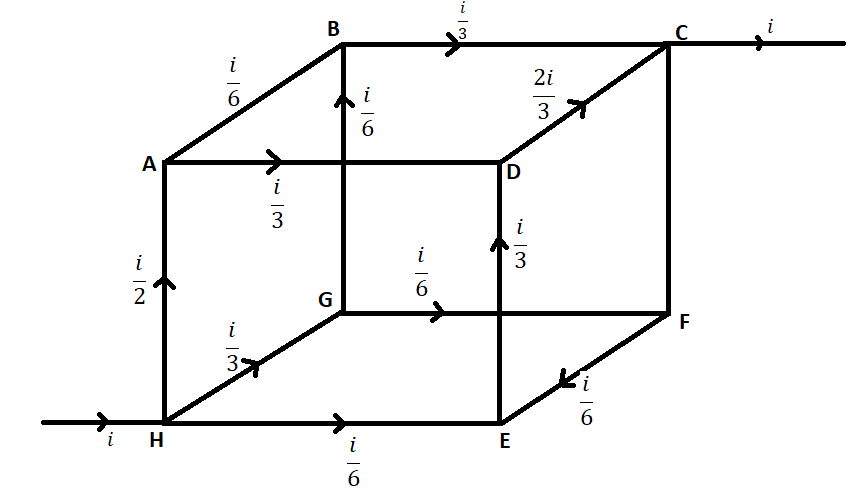
In the box shown current \[i\] enters at \[H\] and leaves at \[C\] . If \[{i_{AB}} = \dfrac{i}{6},\,{i_{DC}} = \dfrac{{2i}}{3},\,{i_{HA}} = \dfrac{i}{2}\,,\,{i_{GF}} = \dfrac{i}{6},\,{i_{HE}} = \dfrac{i}{6},\] choose the branch in which current is zero.

A. BG
B. FC
C. ED
D. None

Answer 1

Hint: In this question we have seen that this is a cubical network. To solve this network first of all we will give the Kirchoff’s Junction Rule and by using it we will find out current flown through every branch of the network and see where the current is zero.
Formula Used:
Kirchoff’s Junction Rule
According to this rule at nodal point the sum of electric currents entering into the node are equal to the sum of electric currents leaving the node.
\[\sum\limits_\,^\, {{i_{entering}} = \sum\limits_\,^\, {{i_{leaving}}} } \]
Given Data: -
\[{i_{AB}} = \dfrac{i}{6},\,{i_{DC}} = \dfrac{{2i}}{3},\,{i_{HA}} = \dfrac{i}{2}\,,\,{i_{GF}} = \dfrac{i}{6},\,{i_{HE}} = \dfrac{i}{6}\]

Step by step solution:
Now we will find the electric current in every branch as follows:
By using Kirchoff’s Junction Rule at point \[H\] current through \[GH\] branch.
\[{i_{GH}} = i - \left( {{i_{HA}} - {i_{HE}}} \right) = i - \left( {\dfrac{i}{2} + \dfrac{i}{6}} \right) = i - \left( {\dfrac{{3i + i}}{6}} \right) = i - \dfrac{{4i}}{6} = \dfrac{i}{3}\]
By using Kirchoff’s Junction Rule at point \[A\] current through \[AD\] branch.
\[{i_{AD}} = {i_{HA}} - {i_{AB}} = \dfrac{i}{2} - \dfrac{i}{6} = \dfrac{i}{3}\]
By using Kirchoff’s Junction Rule at point \[D\] current through \[ED\] branch.
\[{i_{ED}} = {i_{DC}} - {i_{AD}} = \dfrac{{2i}}{3} - \dfrac{i}{3} = \dfrac{i}{3}\]
By using Kirchoff’s Junction Rule at point \[G\] current through \[GB\] branch.
\[{i_{GB}} = {i_{HG}} - {i_{GF}} = \dfrac{i}{3} - \dfrac{i}{6} = \dfrac{i}{6}\]
By using Kirchoff’s Junction Rule at point \[B\] current through \[BC\] branch.
\[{i_{BC}} = {i_{AB}} + {i_{GB}} = \dfrac{i}{6} + \dfrac{i}{6} = \dfrac{i}{3}\]
By using Kirchoff’s Junction Rule at point \[D\] current through \[DC\] branch.
\[{i_{DC}} = {i_{AD}} + {i_{ED}} = \dfrac{i}{3} + \dfrac{i}{3} = \dfrac{{2i}}{3}\]
Here we can observe from calculation above that \[{i_{BC}} = \dfrac{i}{3}\] and \[{i_{DC}} = \dfrac{{2i}}{3}\] are add to make the current \[i\] so there must be zero current in \[FC\] branch.

Hence option \[(B)\] is correct.

Note: - In this question there must be careful use of Kirchoff’s Junction Rule to distribute the electric current at every nodal point. It is very important to note that the current entering into any circuit is always equal to the electric current leaving any circuit.