Question

In the below, \[PQ{\text{ }}||{\text{ }}AB\]and \[PR{\text{ }}||{\text{ }}BC\]. If \[\angle QPR{\text{ }} = {\text{ }}102^\circ ,\] determine \[\angle ABC\]. Give reasons.

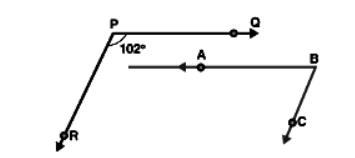
Answer 1

Hint: Extend the line \[AB\] further till intersection and use properties of parallel lines
First, we are going to extend the line \[AB\] until it intersects \[PR\]. Then we are going to find the angle at the point of intersection with help of the properties of the parallel lines which are corresponding angles of parallel lines are equal. Once, we have found that, we know that corresponding angles are supplementary, which means that the sum of their angles is equal to ${180^o}$. Such that we find the required angle with the extended line and then find the required angle.

Complete step by step solution:
We are going to extend the line\[AB\] further till intersection at $G$

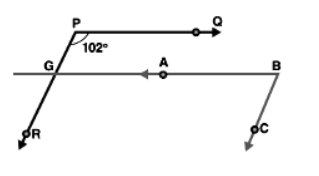
On extending the line, the parallel lines$BC\,\,and\,\,PR$ are getting intersected.
Then, we are given that
$PQ\parallel AB$.
So, from the properties of parallel lines, we know that corresponding angles of parallel lines are equal. It means that
$\angle QPR = \angle BGR = {102^o}$
And since, $PR\parallel BC$
We also know that the corresponding sides are always supplementary, which means the sum of angles is equal to ${180^o}$.
So,
$\angle RCB + \angle CBG = {180^o}$.
Since, we know that $\angle BGR = {102^o}$, we will substitute the value above. Then we get
$\angle CBG = {180^o} - {102^o} = {78^o}$
Since, we know that $\angle CBG$ is just the extended line of line \[AB\], then it implies that

$\angle CBG = \angle ABC$
So, it means that
$\angle ABC = {78^o}$

Note: We should note that only corresponding angles of the parallel line are equal, not only that even alternate angles of the intersected parallel lines are equal which can also be called as vertically opposite angles.