
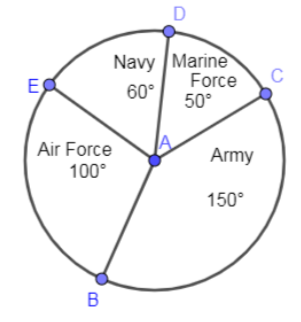
In the below pie diagram, what is the percentage of men volunteered to join the navy force?
(a)$25%$
(b)$21.97%$
(c)$16.67%$
(d)$49%$

Answer
579k+ views
Hint: In the above question, we have given a pie diagram in which different degrees of the circle correspond to different disciplines and we have to find the percentage of men volunteered to join the navy force. This percentage is going to be calculated by dividing the degrees corresponding to the navy to the total degree $\left( {{360}^{\circ }} \right)$ and then multiplying this result of division by 100.
Complete step-by-step solution:
In the above question, we have given the following pie diagram:
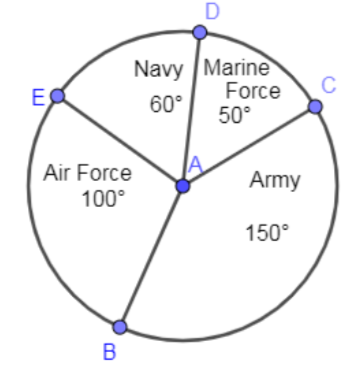
Using this diagram, we have to find the percentage of men who volunteered to join the navy force.
The degrees corresponding to navy force from the pie diagram is ${{60}^{\circ }}$ and the total degrees of the complete pie are equal to addition of all the degrees given in the pie diagram.
Adding all the degrees given in the pie diagram we get,
$\begin{align}
& {{50}^{\circ }}+{{60}^{\circ }}+{{100}^{\circ }}+{{150}^{\circ }} \\
& ={{360}^{\circ }} \\
\end{align}$
The percentage of men volunteered to join navy force is calculated by dividing the degrees corresponding to navy force to the total degrees and then multiplying 100 with this result of division.
$\dfrac{{{60}^{\circ }}}{{{360}^{\circ }}}\times 100$
One zero from numerator and denominator will be cancelled out and we get,
$\dfrac{6}{36}\times 100$
Dividing 6 in the numerator and the denominator of the above expression we get,
$ \dfrac{1}{6}\times 100 $
$=\dfrac{50}{3}=16.67\% $
From the above solution, we have found that $16.67\%$ percentage of men volunteered to join the navy force.
Hence, the correct option is (c).
Note: Instead of solving the total degrees in the above pie diagram by adding all the degrees given in the pie diagram we can use the information that a pie or a circle is making an angle of ${{360}^{\circ }}$ at the center of the circle. By using this information, we can save time in solving the above question in the examination.
We can also cross-check whether the percentage that we are getting is correct or not by multiplying the percentage that we got by ${{360}^{\circ }}$ and then divide this result of multiplication by 100.
$360\left( \dfrac{16.67}{100} \right)$
$\begin{align}
& =\dfrac{6001.2}{100} \\
& =60.012 \\
\end{align}$
By rounding off to the nearest integer we get the degrees corresponding to the navy is ${{60}^{\circ }}$.
Hence, we have verified the percentage that we got in the above solution.
Complete step-by-step solution:
In the above question, we have given the following pie diagram:

Using this diagram, we have to find the percentage of men who volunteered to join the navy force.
The degrees corresponding to navy force from the pie diagram is ${{60}^{\circ }}$ and the total degrees of the complete pie are equal to addition of all the degrees given in the pie diagram.
Adding all the degrees given in the pie diagram we get,
$\begin{align}
& {{50}^{\circ }}+{{60}^{\circ }}+{{100}^{\circ }}+{{150}^{\circ }} \\
& ={{360}^{\circ }} \\
\end{align}$
The percentage of men volunteered to join navy force is calculated by dividing the degrees corresponding to navy force to the total degrees and then multiplying 100 with this result of division.
$\dfrac{{{60}^{\circ }}}{{{360}^{\circ }}}\times 100$
One zero from numerator and denominator will be cancelled out and we get,
$\dfrac{6}{36}\times 100$
Dividing 6 in the numerator and the denominator of the above expression we get,
$ \dfrac{1}{6}\times 100 $
$=\dfrac{50}{3}=16.67\% $
From the above solution, we have found that $16.67\%$ percentage of men volunteered to join the navy force.
Hence, the correct option is (c).
Note: Instead of solving the total degrees in the above pie diagram by adding all the degrees given in the pie diagram we can use the information that a pie or a circle is making an angle of ${{360}^{\circ }}$ at the center of the circle. By using this information, we can save time in solving the above question in the examination.
We can also cross-check whether the percentage that we are getting is correct or not by multiplying the percentage that we got by ${{360}^{\circ }}$ and then divide this result of multiplication by 100.
$360\left( \dfrac{16.67}{100} \right)$
$\begin{align}
& =\dfrac{6001.2}{100} \\
& =60.012 \\
\end{align}$
By rounding off to the nearest integer we get the degrees corresponding to the navy is ${{60}^{\circ }}$.
Hence, we have verified the percentage that we got in the above solution.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE





