Question

In the below figure, \[\vartriangle BEF\] and \[\vartriangle FED\] are two isosceles triangles in the square \[ABCD\].

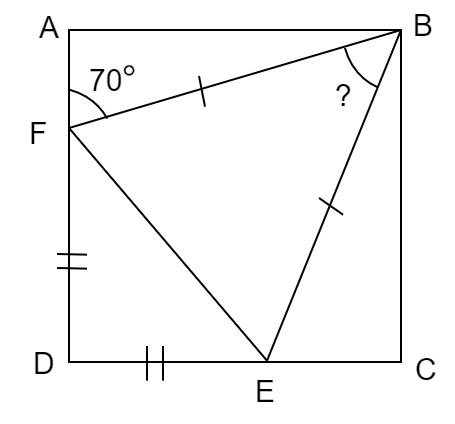
What is the measure of \[\angle FBE\]?
(A) \[{85^ \circ }\]
(B) \[{50^ \circ }\]
(C) \[{65^ \circ }\]
(D) \[{130^ \circ }\]

Answer 1

Hint: To solve this question, we use the property of isosceles triangles, which states that the angles opposite to equal sides are equal. And we use the angle sum property of triangles, which states that the sum of all angles in a triangle is equal to $180^\circ$. And also use the concept of linear pair, that is, Linear pair of angles is actually a special form of adjacent angles where only one condition is necessary that sums up to $180^\circ$. By applying these properties we will find \[\angle FBE\].

Complete answer:
Given, \[\angle AFB = {70^ \circ }\].
In \[\vartriangle FED\], we have \[DE = DF\].
As we know, the angle opposite to equal sides is equal.
\[\therefore \angle DFE = \angle DEF\]
As we know, the sum of all the angles in a triangle is equal to \[{180^ \circ }\].
Therefore, in \[\vartriangle FED\] we have
\[ \Rightarrow \angle FDE + \angle DFE + \angle DEF = {180^ \circ }\]
As, \[ABCD\] is a square. So, \[\angle FDE = {90^ \circ }\].
Therefore, we get
\[ \Rightarrow {90^ \circ } + 2\angle DFE = {180^ \circ }\]
Subtracting both the sides by \[{90^ \circ }\], we get
\[ \Rightarrow 2\angle DFE = {180^ \circ } - {90^ \circ }\]
On simplifying we get,
\[ \Rightarrow 2\angle DFE = {90^ \circ }\]
Dividing both the sides by \[2\], we get
\[ \Rightarrow \angle DFE = {45^ \circ }\]
Now, a linear pair of angles must add up to \[{180^ \circ }\]. Therefore, we get
\[ \Rightarrow \angle AFB + \angle BFE + \angle DFE = {180^ \circ }\]
So, on putting the values, we get
\[ \Rightarrow {70^ \circ } + \angle BFE + {45^ \circ } = {180^ \circ }\]
\[ \Rightarrow \angle BFE + {115^ \circ } = {180^ \circ }\]
Subtracting both the sides by \[{115^ \circ }\], we get
\[ \Rightarrow \angle BFE = {180^ \circ } - {115^ \circ }\]
On simplification, we get
\[ \Rightarrow \angle BFE = {65^ \circ }\]
Now, consider \[\vartriangle BFE\], we have given that \[BF = BE\].
As we know, the angle opposite to equal sides is equal.
\[\therefore \angle BEF = \angle BFE\]
In \[\vartriangle BFE\], we have
\[ \Rightarrow \angle FBE + \angle BEF + \angle BFE = {180^ \circ }\]
Putting the values, we get
\[ \Rightarrow \angle FBE + {65^ \circ } + {65^ \circ } = {180^ \circ }\]
\[ \Rightarrow \angle FBE + {130^ \circ } = {180^ \circ }\]
Subtracting \[{130^ \circ }\] from both the sides, we get
\[ \Rightarrow \angle FBE = {50^ \circ }\]
Therefore, \[\angle FBE\] is \[{50^ \circ }\]. So, option (B) is correct.

Note:
In an isosceles triangle two sides are of equal length. Angles opposite to equal sides in an isosceles triangle are always of equal measures. Also, note that all the three angles situated within the isosceles triangle are acute, which signifies that the angles are less than \[{90^ \circ }\].