Question

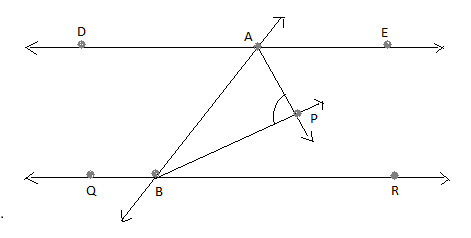
In the below figure, if $DE\parallel QR$ and $AP$ and $BP$ are the bisectors of $\angle EAB$ and $\angle RBA$ , then find out the value of $\angle APB$ .

Answer 1

Hint: In this problem we have to find out the value of $\angle APB$ .
Let observe the sides and angles of the triangle.
Recall the transversal and consecutive interior angles.
Then apply the formula and do some simplification.
Finally we get our required answer.

Formula used: The sum of the three angles of any triangle,$\vartriangle ABC$ is equal to 180 degrees.
That is, $\angle A + \angle B + \angle C = {180^ \circ }$

Complete step-by-step answer:
It is given that the$DE$ is parallel to $QR$
The line $AB$ crossed the parallel lines
Here,$AP$ is the bisectors of $\angle EAB$ and $BP$ is the bisectors of $\angle RBA$
When the two lines being crossed are parallel lines the consecutive interior angles sum up to${180^ \circ }$
Here, $\angle EAB$ and $\angle RBA$ are the consecutive interior angles.
The sum of these two angles gives \[180\] degree.
Then, $\angle EAB + \angle RBA = {180^ \circ }$
It can be rewritten as $\angle EAB + \angle RBA = 2 \times {90^ \circ }$
Bringing the constant 2 into the left hand side, it becomes
$\dfrac{1}{2}\left( {\angle EAB + \angle RBA} \right) = {90^ \circ }$
Now,$AP$ is the bisectors of$\angle EAB$ and $BP$ is the bisectors of $\angle RBA$
$\angle PAB + \angle PBA = {90^ \circ }$
Consider, the triangle$\vartriangle PAB$,
The sum of the three angles of any triangle is equal to \[180\] degrees.
Here, $\angle PAB + \angle PBA + \angle APB = {180^ \circ }$
Replace \[\angle PAB + \angle PBA\] by \[{90^ \circ }\]
Then the expression becomes,
${90^ \circ } + \angle APB = {180^ \circ }$
Bringing ${90^ \circ }$ to right side,
$\angle APB = {180^ \circ } - {90^ \circ }$
On subtracting we get, $\angle APB = {90^ \circ }$

Therefore $\angle APB = {90^ \circ }$

Note: When parallel lines get crossed by another line is called transversal.
The pair angles on one side of transversal but inside the two lines are called consecutive interior angles.
When the two lines being crossed are parallel lines the consecutive interior angles sum up to ${180^ \circ }$.
The angle of the straight line is ${180^ \circ }$