Question

In the below figure, find the value of ${{x}^{\circ }}$?

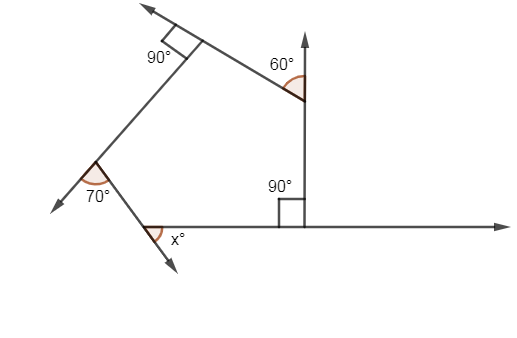
Answer 1

Hint: First of all, we are going to mark the intersection of the lines for the better explanation. Now, to find the value of x, we are going to use the linear pair concept in which we know the angle a line has ${{180}^{\circ }}$ and a line is drawn on that line then the sum of the two sides of the angles is equal to ${{180}^{\circ }}$. Also, we are going to use the property that sum of all the interior angles of a polygon is equal to $\left( n-2 \right)\left( {{180}^{\circ }} \right)$ where n is the number of sides present in the polygon.

Complete step by step solution:
The figure given in the above problem is as follows:

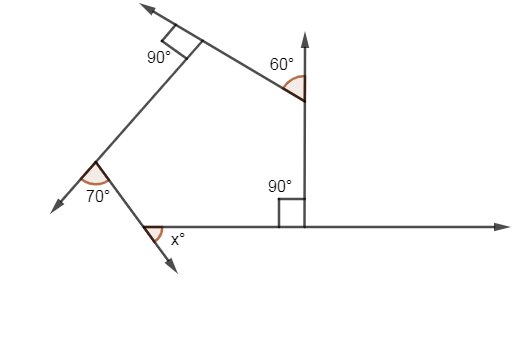
Now, we are going to mark the intersections of the lines as follows:

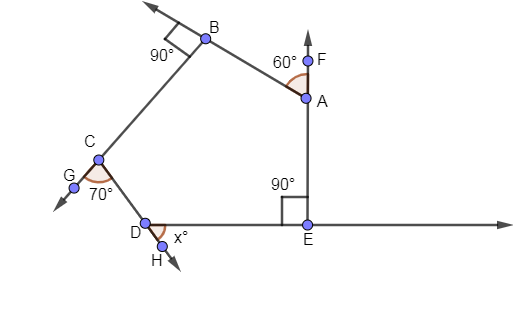
From the above figure, we are asked to find the value of x which we are going to find as follows:
First of all, we are going to find $\angle BAE$ which we are going to find using the linear pair concept. As AB is forming a linear pair on the line EF so the sum of angles BAE and angle BAF is equal to ${{180}^{\circ }}$. Doing this summation of the angles we get,
$\angle BAE+\angle BAF={{180}^{\circ }}$
From the figure, you can see that $\angle BAF={{60}^{\circ }}$ so using this angle in the above equation we get,
$\begin{align}
  & \angle BAE+{{60}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle BAE={{180}^{\circ }}-{{60}^{\circ }} \\
 & \Rightarrow \angle BAE={{120}^{\circ }} \\
\end{align}$
Similarly, we are going to find $\angle BCD$ by using this linear pair concept.
$\angle BCD+\angle GCD={{180}^{\circ }}$
From the figure, you can see that $\angle GCD={{70}^{\circ }}$ so using this angle in the above equation we get,
$\begin{align}
  & \angle BCD+{{70}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle BCD={{180}^{\circ }}-{{70}^{\circ }} \\
 & \Rightarrow \angle BCD={{110}^{\circ }} \\
\end{align}$
We know that, sum of the interior angles of the polygon is equal to:
$\left( n-2 \right)\left( {{180}^{\circ }} \right)$
In the above formula, “n” is the number of sides of the polygon. In the above figure, the polygon ABCDE has 5 sides so the value of n as 5 in the above formula we get,
$\begin{align}
  & \left( 5-2 \right)\left( {{180}^{\circ }} \right) \\
 & =3\left( {{180}^{\circ }} \right) \\
 & ={{540}^{\circ }} \\
\end{align}$
Now, taking the sum of all the interior angles of the polygon and equating that sum to ${{540}^{\circ }}$.
$\angle ABC+\angle BCD+\angle CDE+\angle DEA+\angle BAE={{540}^{\circ }}$
Substituting $\angle BAE={{120}^{\circ }}$,$\angle BCD={{110}^{\circ }}$,$\angle ABC={{90}^{\circ }},\angle DEA={{90}^{\circ }}$ in the above equation we get,
$\begin{align}
  & {{90}^{\circ }}+{{110}^{\circ }}+\angle CDE+{{90}^{\circ }}+{{120}^{\circ }}={{540}^{\circ }} \\
 & \Rightarrow {{410}^{\circ }}+\angle CDE={{540}^{\circ }} \\
 & \Rightarrow \angle CDE={{540}^{\circ }}-{{410}^{\circ }} \\
 & \Rightarrow \angle CDE={{130}^{\circ }} \\
\end{align}$
Now, again applying linear pair concept in finding the value of x as follows:
$\angle CDE+\angle EDH={{180}^{\circ }}$
Substituting the value of $\angle CDE={{130}^{\circ }}$ in the above equation we get,
$\begin{align}
  & {{130}^{\circ }}+\angle EDH={{180}^{\circ }} \\
 & \Rightarrow \angle EDH={{180}^{\circ }}-{{130}^{\circ }} \\
 & \Rightarrow \angle EDH={{50}^{\circ }} \\
\end{align}$
Hence, we have found the value of x as ${{50}^{\circ }}$.

Note: The mistake that could be possible in the above problem is that you might write the sum of the interior angles of the polygon as ${{360}^{\circ }}$ because sum of the interior angles of the quadrilateral is ${{360}^{\circ }}$ so you might think that interior angles of quadrilateral is also equal to ${{360}^{\circ }}$. So, make sure you won’t make this mistake in the above solution.