
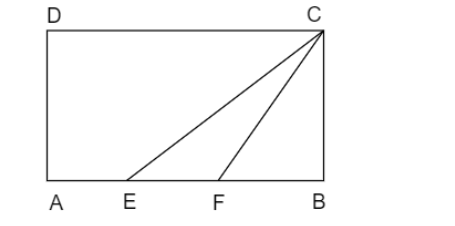
In the below diagram, $ABCD$ is a rectangle with $AE=EF=FB$ . What is the ratio of the areas of the $\Delta CEF$ and that of the rectangle?
A. $\dfrac{1}{6}$
B. $\dfrac{1}{8}$
C. $\dfrac{1}{9}$
D. None of these

Answer
501.9k+ views
Hint: Here we have been given a rectangle with some points on it which forms a triangle within the rectangle and we have to find the ratio of area between a triangle and the rectangle. Firstly as there is no dimension given we have to take the values of the side as their name. Then we will get the area of the desired triangle by subtracting the area of two triangles that enclosed it. Finally we will form a ration between the area of the rectangle and the triangle and get our desired answer.
Complete step by step solution:
We have been given that,
$AE=EF=FB$…..$\left( 1 \right)$
The figure is given as below:
We have to find the area of the $\Delta CEF$ .
The formula of area of triangle is as follows:
Area $A=\dfrac{1}{2}\times b\times h$….$\left( 2 \right)$
Where, $b=$ Base and $h=$ Height
From the figure it is clear that when we subtract the area of $\Delta CFB$ from the area of $\Delta CEB$ we will get the area of $\Delta CEF$ .
So we can write the above statement as follows:
Area of $\Delta CEF=$ Area of $\Delta CEB-$ Area of $\Delta CFB$
Using equation (2) above we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times b\times h-\dfrac{1}{2}\times b\times h$…..$\left( 3 \right)$
From the figure the base and height of $\Delta CEB$ is $EB,BC$ respectively and base and height of $\Delta CFB$ is $FB,BC$ respectively.
Using above value in equation (3) we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times EB\times BC-\dfrac{1}{2}\times FB\times BC$…..$\left( 4 \right)$
From equation (1) we can say that side $AB$ is divided into three parts so we can write,
$EB=\dfrac{2}{3}AB$ and $FB=\dfrac{1}{3}AB$
On replacing above value in equation (4) we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times \left( \dfrac{2}{3}AB \right)\times BC-\dfrac{1}{2}\times \left( \dfrac{1}{3}AB \right)\times BC$
Area of $\Delta CEF=$ $\dfrac{1}{3}\times AB\times BC-\dfrac{1}{6}\times AB\times BC$
On taking L.C.M we get,
Area of $\Delta CEF=$ $\dfrac{2AB\times BC-AB\times BC}{6}$
Area of $\Delta CEF=$ $\dfrac{1}{6}\times AB\times BC$…..$\left( 5 \right)$
Now we will find area of rectangle by below formula,
Area of rectangle$=l\times b$….$\left( 6 \right)$
From figure we get
$l=AB$ and $b=BC$
Replace value in equation (6) we get,
Area of rectangle $ABCD=AB\times BC$….$\left( 7 \right)$
Next on dividing equation (5) by equation (7) we get,
Area of triangle/ Area of rectangle $=\dfrac{\dfrac{1}{6}\times AB\times BC}{AB\times BC}$
Area of triangle/ Area of rectangle $=\dfrac{1}{6}$
Hence the correct option is (A).
So, the correct answer is “Option A”.
Note: A rectangle is a quadrilateral with four sides and four right angles where opposite sides are of the same length. A rectangle is cyclic as all its corners lie on a single circle. It has two lines of reflectional symmetry and rotational symmetry of order $2$ . A triangle is a polygon with three sides and three edges; it is a very basic shape in geometry.
Complete step by step solution:
We have been given that,
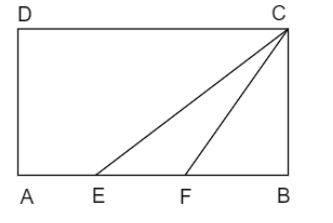
$AE=EF=FB$…..$\left( 1 \right)$
The figure is given as below:

We have to find the area of the $\Delta CEF$ .
The formula of area of triangle is as follows:
Area $A=\dfrac{1}{2}\times b\times h$….$\left( 2 \right)$
Where, $b=$ Base and $h=$ Height
From the figure it is clear that when we subtract the area of $\Delta CFB$ from the area of $\Delta CEB$ we will get the area of $\Delta CEF$ .
So we can write the above statement as follows:
Area of $\Delta CEF=$ Area of $\Delta CEB-$ Area of $\Delta CFB$
Using equation (2) above we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times b\times h-\dfrac{1}{2}\times b\times h$…..$\left( 3 \right)$
From the figure the base and height of $\Delta CEB$ is $EB,BC$ respectively and base and height of $\Delta CFB$ is $FB,BC$ respectively.
Using above value in equation (3) we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times EB\times BC-\dfrac{1}{2}\times FB\times BC$…..$\left( 4 \right)$
From equation (1) we can say that side $AB$ is divided into three parts so we can write,
$EB=\dfrac{2}{3}AB$ and $FB=\dfrac{1}{3}AB$
On replacing above value in equation (4) we get,
Area of $\Delta CEF=$ $\dfrac{1}{2}\times \left( \dfrac{2}{3}AB \right)\times BC-\dfrac{1}{2}\times \left( \dfrac{1}{3}AB \right)\times BC$
Area of $\Delta CEF=$ $\dfrac{1}{3}\times AB\times BC-\dfrac{1}{6}\times AB\times BC$
On taking L.C.M we get,
Area of $\Delta CEF=$ $\dfrac{2AB\times BC-AB\times BC}{6}$
Area of $\Delta CEF=$ $\dfrac{1}{6}\times AB\times BC$…..$\left( 5 \right)$
Now we will find area of rectangle by below formula,
Area of rectangle$=l\times b$….$\left( 6 \right)$
From figure we get
$l=AB$ and $b=BC$
Replace value in equation (6) we get,
Area of rectangle $ABCD=AB\times BC$….$\left( 7 \right)$
Next on dividing equation (5) by equation (7) we get,
Area of triangle/ Area of rectangle $=\dfrac{\dfrac{1}{6}\times AB\times BC}{AB\times BC}$
Area of triangle/ Area of rectangle $=\dfrac{1}{6}$
Hence the correct option is (A).
So, the correct answer is “Option A”.
Note: A rectangle is a quadrilateral with four sides and four right angles where opposite sides are of the same length. A rectangle is cyclic as all its corners lie on a single circle. It has two lines of reflectional symmetry and rotational symmetry of order $2$ . A triangle is a polygon with three sides and three edges; it is a very basic shape in geometry.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




