Question

In the arrangement shown in figure, the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed of

A. $2u\cos \theta $
B.$\dfrac{u}{\cos \theta }$
C.$\dfrac{2u}{\cos \theta }$
D.$u\cos \theta $

Answer 1

Hint: As a first step, make necessary constructions in the given diagram and thus consider a triangle. Apply Pythagorean theorem to get an expression. Differentiate with respect to time and then do necessary substitutions. You may then use basic trigonometry to get the required velocity in terms of u and $\cos \theta $.

Complete Step by step solution:
Let the velocity with which mass M moves upwards be v and we are already given that ends on the string P and Q move downwards with velocity u. So, every point on the string moves with the same velocity u.

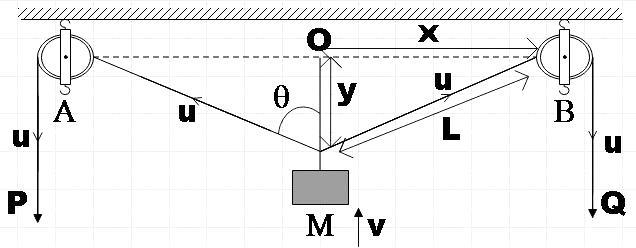
Consider the triangle MOB. By Pythagorus theorem we have,
${{x}^{2}}+{{y}^{2}}={{L}^{2}}$

Differentiating both sides with respect to time, we get,
$2y\dfrac{dy}{dt}=2L\dfrac{dL}{dt}$

Since x remains constant at all points of time.
We know that $\dfrac{dy}{dt}=v$and$\dfrac{dL}{dt}=u$,
$\Rightarrow y\times v=L\times u$
$\Rightarrow v=\dfrac{L}{y}\times u$

But from the figure we see that,
$\cos \theta =\dfrac{y}{L}$
$\therefore v=\dfrac{u}{\cos \theta }$

Therefore, we found that the mass M moves upwards with a speed of$\dfrac{u}{\cos \theta }$.

Hence, option B is found to be the correct answer.

Note:
We also have a very simple alternative method to solve this problem which doesn’t involve calculus. For that we could resolve the velocity v of the mass M into its components. We would find the cosine component along the string. But as the ends have velocity u downward, every point on the string should have the same velocity. Thus we could equate both to get,
$v\cos \theta =u$
$\therefore v=\dfrac{u}{\cos \theta }$