Question

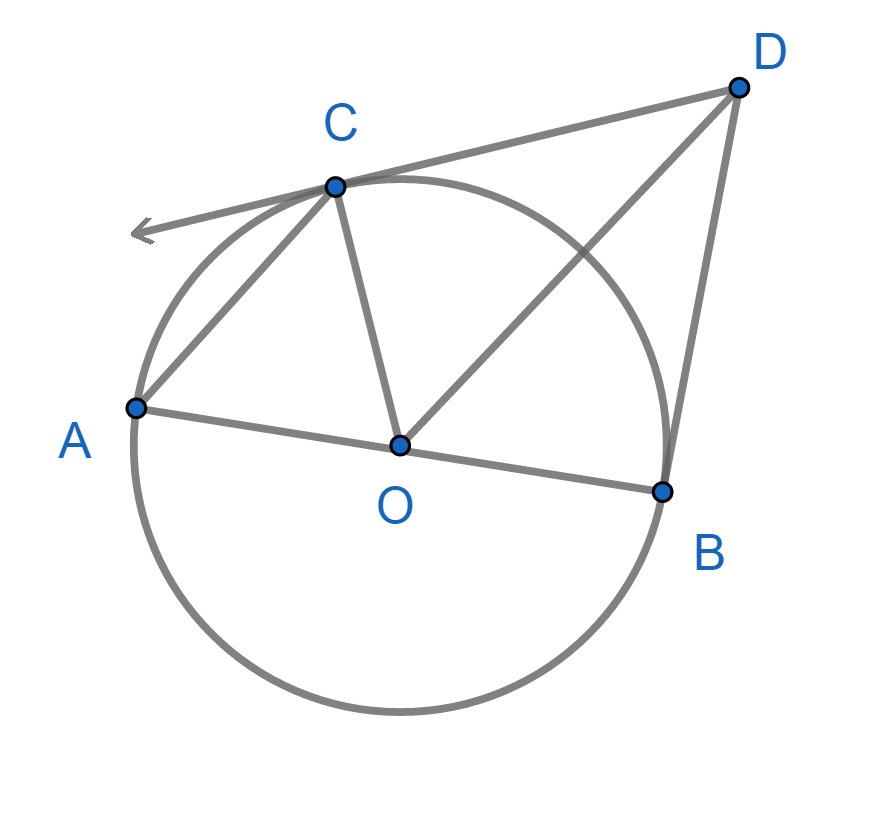
In the adjoining figure, O is the center of the circle and AB is the diameter. At C on the circle the tangent CD is drawn. The line BD is tangent to the circle at point B. Show that segment OD $\parallel $ chord AC.

Answer 1

Hint: We are given a circle with center O, we need to show that segment OD $\parallel $ to chord AC. We will need the knowledge that tangents from the same exterior are equal in length, we will first claim that $\Delta OCD\text{ and }\Delta BOD$ are congruent then we get $\angle COD=\angle BOD$ . After this we use that angle opposite to equal sides are equal in length and also use that if an alternate pair of angles are equal then those lines are parallel.

Complete step-by-step solution:
We are given that, we have a circle with center O.
We are also given that AB is the diameter of the circle and at point C we have tangent CD and also we have that BD is tangent from B.
We know that two tangents from the same external point are always equal in length.
We are given CD and BD are tangent from the same point D. So, CD = BD. . . . . . . . . . . . . . (1).
Considering $\Delta OCD\text{ and }\Delta BOD$ we will claim that they are congruent.
In $\Delta OCD\text{ and }\Delta BOD$,
OC = OB (both are radius)
CD = BD (using 1)
OD = OD (common sides).
So by side side side criteria, these two triangles are congruent. Now, as we know, the corresponding parts of the congruent triangles are equal. So we have, $\angle COD=\angle BOD$.
Let's take them as x.
So we have $\angle COD=\angle BOD=x\ldots \ldots \ldots \left( 2 \right)$.
Now as we can see that OA and OC are both radii, so OA = OC (both are radii) so we get, $\angle OAC=\angle OCA$. (Angles opposite to equal sides are equal).
We name it as y, so $\angle OAC=\angle OCA=y\ldots \ldots \ldots \left( 3 \right)$.

We know that the exterior angle sum property says that the measure of each exterior angle is equal to the sum of the opposite and non-adjacent angle. So in $\Delta ACO$ we get, \[\angle COB=\angle OAC+\angle OCA\].
\[\angle COB\] can be written as the sum of $\angle COD=\angle BOD$
So we get, $\angle COD+\angle BOD=\angle OAC+\angle OCA$.
Using (2) and (3) here we get, $x+x=y+y\Rightarrow 2x=2y$.
Simplifying we get, x = y.
So we get $\angle COD=\angle OCA$.
For the line OD and these angles are a pair of alternate interior angles.
Since the pair of alternate interior angles is equal so we get, segment OD $\parallel $ chord AC.

Note: Remember that, corresponding side and angle are only equal if our given triangles are congruent, not any arbitrary pair. If side or angles are equal, that is if $\Delta ABC\cong \Delta GHI$ then AB = GH, BC = HI and AC = GI, we cannot say, AC = GH because C is not corresponding to H. So always we need to be precise.