Question

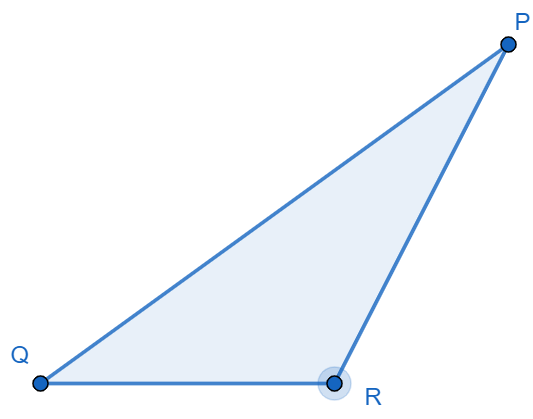
In the adjoining figure: Name the vertex opposite to side \[PQ\].

Answer 1

Hint: In order to find the opposite vertex of the given side \[PQ\] from the \[\Delta PQR\], firstly, we must consider all the sides and the vertices. To find the opposite vertex of \[PQ\], we must find such vertex from the \[\Delta PQR\] such that it does not have any connection with the given particular side which simply means that it is not at all connected with the side \[PQ\].

Complete step by step answer:
Now let us learn about the properties of a triangle. The angle-sum property of a triangle states that the sum of interior angles of a triangle is equal to \[{{180}^{\circ }}\]. The sum of lengths of any two sides of a triangle is greater than the third side of a triangle. There are six types of triangles. They are: equilateral triangle, isosceles triangle, scalene triangle, obtuse angled, right angled and acute angled triangle. The area of a triangle can be found by \[\dfrac{1}{2}bh\] and the perimeter of a triangle can be found by sum of lengths of all three sides.
Now let us find the vertex that is opposite to the side \[PQ\] from the triangle \[\Delta PQR\].
Opposite vertex to a side is nothing but the vertex that is not adjacent to the side.
From the figure, we can observe that the vertices \[P\] and \[Q\] are adjacent to the side \[PQ\]. In fact, we can say that the side \[PQ\] is formed by those two vertices.
So, the only vertex that is not adjacent to the side \[PQ\] is \[R\].
\[\therefore \] The vertex opposite to side \[PQ\] is \[R\].

Note: We can always have a note that this opposite and the adjacent theorems are applicable to all of the triangle. We must also note that while finding the area of the triangle, the height of the triangle depends upon the type of the triangle as the height of an obtuse angled triangle lies outside whereas the height of an equilateral triangle lies inside the triangle.