
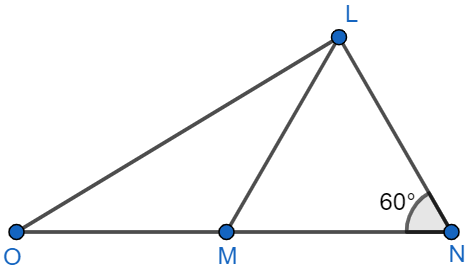
In the adjoining figure, \[LM\text{ }=\text{ }MO\] and \[LN\text{ }=\text{ }NM\]. Find: a) $\angle NLM$ b) $\angle LOM$.

Answer
606k+ views
Hint: We will use a concept that the angle opposite to the equal sides of the triangles are of equal measurement. For example, if ABC is a triangle, with $AB=AC$ then we can say that $\angle ABC=\angle ACB$. We will also use the angle sum property of triangles which state that the sum of all the angles of the triangle is equal to 180.
Complete step-by-step answer:
It is given in the question that $LM=MO$ and $LN=NM$ then we will have to find the angles $\angle NLM$ and $\angle LOM$.
We know that sum of all angles of a triangle is equal to 180 degree, so, in $\Delta LNM$, we have $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$.
We also know that angles opposite to the sides of equal length are of equal measurement value. In $\Delta LMN$, we have side \[LN\text{ }=\text{ }NM\], so from this, we can say that $\angle NLM=\angle LMN$.
On putting these value in the equation $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$ we get,
${{60}^{{}^\circ }}+\angle NLM+\angle NLM={{180}^{{}^\circ }}$, solving further, we get,
$2\angle NLM={{180}^{{}^\circ }}-{{60}^{{}^\circ }}$, therefore, we get finally,
\[\angle NLM=\dfrac{{{120}^{{}^\circ }}}{2}={{60}^{{}^\circ }}\].
Also, we get $\angle NML={{60}^{{}^\circ }}$.
We know that sum of linear pairs is equal to 180, and angles $\angle LMO\text{ }and\text{ }\angle LMN$ are forming linear pair, therefore,
$\angle LMO+\angle LMN={{180}^{{}^\circ }}$, putting the value $\angle NML={{60}^{{}^\circ }}$, we get,
$\angle LMO+{{60}^{{}^\circ }}={{180}^{{}^\circ }}$, therefore,
$\angle LMO={{180}^{{}^\circ }}-{{60}^{{}^\circ }}={{120}^{{}^\circ }}$.
Now, in $\Delta LMO$, we have sum of all three angles of the triangle as 180, it means $\angle LOM+\angle OML+\angle MLO={{180}^{{}^\circ }}$. Also, $\angle LOM=\angle MLO$ as they are angles opposite to equal sides, therefore we get,
$\angle LOM+{{120}^{{}^\circ }}+\angle LOM={{180}^{{}^\circ }}$, solving further, we get
$2\angle LOM={{180}^{{}^\circ }}-{{120}^{{}^\circ }}={{60}^{{}^\circ }}$, therefore, we finally get,
$\angle LOM=\dfrac{{{60}^{{}^\circ }}}{2}={{30}^{{}^\circ }}$.
Thus we get \[\angle NLM={{60}^{{}^\circ }}\] and $\angle LOM={{30}^{{}^\circ }}$.
Note: Usually students do miss-calculation in adding the angles of the triangle and it is enough to waste our all effort to solve this question. Generally, these silly mistakes are not traced even while revision, thus it is recommended to do calculation steps without mistakes. Sometimes students might think that triangle LMN is an equilateral triangle just by looking at it and then compute the angle, but it is not necessarily true always.
Complete step-by-step answer:
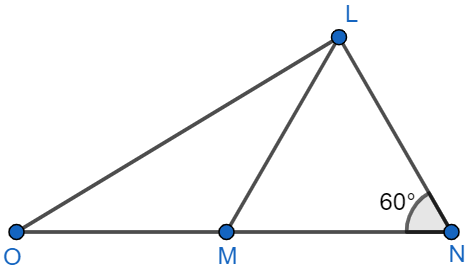
It is given in the question that $LM=MO$ and $LN=NM$ then we will have to find the angles $\angle NLM$ and $\angle LOM$.

We know that sum of all angles of a triangle is equal to 180 degree, so, in $\Delta LNM$, we have $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$.
We also know that angles opposite to the sides of equal length are of equal measurement value. In $\Delta LMN$, we have side \[LN\text{ }=\text{ }NM\], so from this, we can say that $\angle NLM=\angle LMN$.
On putting these value in the equation $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$ we get,
${{60}^{{}^\circ }}+\angle NLM+\angle NLM={{180}^{{}^\circ }}$, solving further, we get,
$2\angle NLM={{180}^{{}^\circ }}-{{60}^{{}^\circ }}$, therefore, we get finally,
\[\angle NLM=\dfrac{{{120}^{{}^\circ }}}{2}={{60}^{{}^\circ }}\].
Also, we get $\angle NML={{60}^{{}^\circ }}$.
We know that sum of linear pairs is equal to 180, and angles $\angle LMO\text{ }and\text{ }\angle LMN$ are forming linear pair, therefore,
$\angle LMO+\angle LMN={{180}^{{}^\circ }}$, putting the value $\angle NML={{60}^{{}^\circ }}$, we get,
$\angle LMO+{{60}^{{}^\circ }}={{180}^{{}^\circ }}$, therefore,
$\angle LMO={{180}^{{}^\circ }}-{{60}^{{}^\circ }}={{120}^{{}^\circ }}$.
Now, in $\Delta LMO$, we have sum of all three angles of the triangle as 180, it means $\angle LOM+\angle OML+\angle MLO={{180}^{{}^\circ }}$. Also, $\angle LOM=\angle MLO$ as they are angles opposite to equal sides, therefore we get,
$\angle LOM+{{120}^{{}^\circ }}+\angle LOM={{180}^{{}^\circ }}$, solving further, we get
$2\angle LOM={{180}^{{}^\circ }}-{{120}^{{}^\circ }}={{60}^{{}^\circ }}$, therefore, we finally get,
$\angle LOM=\dfrac{{{60}^{{}^\circ }}}{2}={{30}^{{}^\circ }}$.
Thus we get \[\angle NLM={{60}^{{}^\circ }}\] and $\angle LOM={{30}^{{}^\circ }}$.
Note: Usually students do miss-calculation in adding the angles of the triangle and it is enough to waste our all effort to solve this question. Generally, these silly mistakes are not traced even while revision, thus it is recommended to do calculation steps without mistakes. Sometimes students might think that triangle LMN is an equilateral triangle just by looking at it and then compute the angle, but it is not necessarily true always.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




