Question

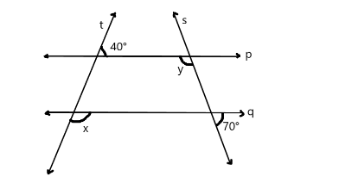
In the adjoining figure line $ p || $ line $ q $ . Line $ t $ and line $ s $ are transversals. Find the measure of angle $ x $ and angle $ y $ using the measure of angles given in the figure.

Answer 1

Hint: In order to find the value of angle $ x $ and angle $ y $ , first name the angles for ease, then use the properties of parallel lines, like alternate interior angles, opposite angles, co-interior angles, etc.
Find the best suitable relations between the angles, and get the values.

Complete step by step solution:
We are given with two parallel lines as line $ p || $ $ q $ in which Line $ t $ and line $ s $ are transversals.
Name the points of the figures first:

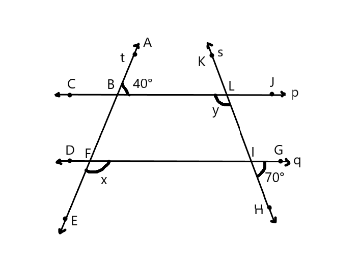
Using the properties of parallel lines and transversal, we get:
 $ \angle ABL = \angle AFI = {40^ \circ } $ (Corresponding Angles)
Now, $ \angle AFI + \angle EFI = {180^ \circ } $ (Linear pair)
Substitute the values of $ \angle AFI = {40^ \circ } $ and $ \angle EFI = x $ in the above equation and solving for $ x $ , we get:
 $
  \angle AFI + \angle EFI = {180^ \circ } \\
  {40^ \circ } + x = {180^ \circ } \\
  x = {180^ \circ } - {40^ \circ } \\
  x = {140^ \circ } \;
  $
And, we get $ x = {140^ \circ } $
Similarly, for the other value $ y $ , using the properties:
 $ \angle BLI = \angle LIG = y $ (Alternate Interior Angles)
Now, $ \angle LIG + \angle GIH = {180^ \circ } $ (Linear pair)
Substitute the values of $ \angle LIG = y $ and $ \angle GIH = {70^ \circ } $ in the above equation and solving for $ y $ , we get:
\[
  \angle LIG + \angle GIH = {180^ \circ } \\
  y + {70^ \circ } = {180^ \circ } \\
  y = {180^ \circ } - {70^ \circ } \\
  y = {110^ \circ } \;
 \]
And, we get $ y = {110^ \circ } $
Therefore, the value of $ x $ and $ y $ for the figure is $ {140^ \circ } $ and $ {110^ \circ } $ .

Note: Properties of parallel lines and transversals are:
I.Corresponding Angles, Ex: $ \angle ABL,\angle AFI $ and $ \angle EFG,\angle EBJ $ , etc.
II.Alternate Interior Angles, Ex: $ \angle CBF,\angle BFI $ and $ \angle JLI,\angle LIF $ , etc.
III.Opposite Angles, Ex: $ \angle ABL,\angle CBF $ and $ \angle GIH,\angle LIF $ , etc.
IV.Linear Pair, Ex: $ \angle KLJ,\angle JLI $ , etc.