Question

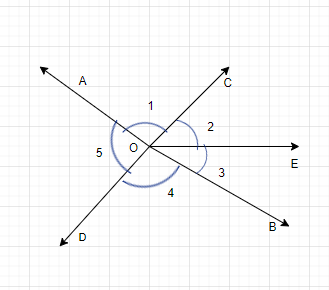
In the adjoining figure,
i) Is $\angle 1$ adjacent to $\angle 2$?
ii) Is $\angle AOC$ adjacent to $\angle AOE$?
iii) Do $\angle COE$ and$\angle EOD$form a linear pair?
iv) Are $\angle BOD$ and$\angle DOA$ supplementary?
v) Is $\angle 1$ vertically opposite to$\angle 4$?
vi) What is vertically opposite angle of $\angle 5$

Answer 1

Hint: In this question it has been asked various questions about angles and their properties. So before answering the question we should know what are the properties of these types of angles. So first we should know that adjacent angles are those angles which are next to each other to prove two angles are adjacent one should know that these angles have the same vertex, a common arm, and the non-common arms should be opposite to the common arm. Next, one should know about supplementary angles; these angles are those whose sum adds up to ${180^ \circ }$. Next, we should know that linear pair angles are those angles whose sum adds up to ${180^ \circ }$ but occur in pairs. Next, up on the list are vertically opposite angles; these are those angels who are opposite to one another but are cut by vertical lines.

Complete step by step answer:
In (i) it is asked that,
Is $\angle 1$ adjacent to $\angle 2$. Yes, it is adjacent to angle $\angle 2$ because as we know adjacent literal meaning is next to one another so we can see in the diagram $\angle 1$ is adjacent to $\angle 2$, also mathematically it is true because they have same vertex, one common arm and their common arms are on opposite sides of the non-common arm. Hence, $\angle 1$ is adjacent to $\angle 2$.
In (ii) it is asked that,
Is $\angle AOC$ adjacent to $\angle AOE$
Well in this case it is not so as we can see in the figure, first they are not next to each other and second they don’t have their common arm opposite to non-common arm.
In (iii) it is asked that,
Do $\angle COD$ and $\angle EOD$ form a linear pair,
Yes, it is a linear pair because linear pairs consist of angle which forms total of${180^ \circ }$ and are in pair, and as we can see in the question $\angle COE$ and$\angle EOD$ form a total of ${180^ \circ }$ and in pair so, it forms a linear pair.
In (iv) it is asked that,
Are $\angle BOD$ and $\angle DOA$ supplementary.
Yes, they are supplementary because as we know that supplementary angles are those angles whose sum adds up to ${180^ \circ }$ and as we can see in the question. Thus they form supplementary angles. In fact, they are linear pairs too.
In (v) it is asked that,
Is $\angle 1$ vertically opposite to $\angle 4$.
Yes, they are vertically opposite angles because as we know vertically opposite angles are those angles who are opposite to each other and are cut by two vertical lines. As we can see in the question it is so, thus it is true.
In (vi) it is asked that,
What is vertically opposite to $\angle 5$.
As it is mentioned above that vertically opposite angles are those angles who are opposite to each other and are cut by vertical lines. So by these conditions the vertically opposite angle to $\angle 5$ is $\angle BOC$ ($\angle 2 + \angle 3$). As satisfied by the conditions.

Note: In this question it should be noted that we have used various properties of angles so before the solution one should know about these properties. By these basic properties one should be able to answer questions of such types.