Question

In the adjoining figure, $\angle OAB = 30^\circ $ and $\angle OCB = 57^\circ ,\angle AOC = $? & $\angle BOC = $?

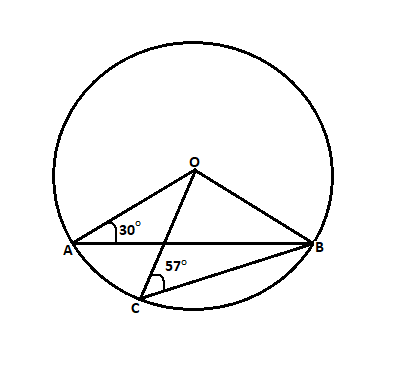
A.$\angle AOC = 120^\circ $& $\angle BOC = 66^\circ $
B.$\angle AOC = 54^\circ $&$\angle BOC = 57^\circ $
C.$\angle AOC = 30^\circ $&$\angle BOC = 57^\circ $
D.$\angle AOC = 54^\circ $&$\angle BOC = 66^\circ $

Answer 1

Hint: In this question we can see two isosceles triangles which implies that the angles opposite to their equal sides will be equal. So, by this we can find the value of $\angle AOB$ and $\angle BOC$
So, then by subtracting $\angle BOC$ from $\angle AOB$, we will get our answer.

Complete step by step solution:
First of all we will start this question by listing the information given in the question.
So, it is given in the question that
There is a circle with center $O$
And $\angle OAB = 30^\circ ,\angle OCB = 57^\circ $
So, first of all we will consider the triangle $\vartriangle OAB$
In this triangle we can clearly see that the sides $OA$ and $OB$ are equal, because they are nothing but the radiuses of the circle.
So, $OA = OB$
$ \Rightarrow \angle OAB = \angle OBA$ (Because in a triangle angles opposite to equal sides are equal)
 $ \Rightarrow \angle OAB = \angle OBA = 30^\circ $ (As it is given that$\angle OAB = 30^\circ $)
Now, as we know that sum of all the angles of a triangle is equal to $180^\circ $
$ \Rightarrow \angle OAB + \angle OBA + \angle AOB = 180^\circ $
So, after putting the corresponding values we get
$
   \Rightarrow 30^\circ + 30^\circ + \angle AOB = 180^\circ \\
   \Rightarrow \angle AOB = 180^\circ - 60^\circ \\
 $
$ \Rightarrow \angle AOB = 120^\circ $ ……..(i)
Now, we will consider the second triangle that is $\vartriangle OBC$
Here also we can clearly see that the side $OC$and $OB$ are equal, because they are nothing but the radiuses of the circle.
So, similarly we can say the angles opposite to these sides will be equal, because in a triangle the angles opposite to equal sides are equal.
$ \Rightarrow \angle OBC = \angle OCB = 57^\circ $ (As it is given that$\angle OCB = 57^\circ $)
Now, as we know that sum of all the angles of a triangle is equal to $180^\circ $
$ \Rightarrow \angle OBC + \angle OCB + \angle BOC = 180^\circ $
So, after putting the corresponding values we get
$
   \Rightarrow 57^\circ + 57^\circ + \angle BOC = 180^\circ \\
   \Rightarrow \angle BOC = 180^\circ - 114^\circ \\
 $
$ \Rightarrow \angle BOC = 66^\circ $ ………(ii)
Now, if we consider the $\angle AOB$
We know that $\angle AOB = \angle AOC + \angle BOC$
So, by putting the corresponding values from equation (i) and (ii) we get
$
   \Rightarrow 120^\circ = \angle AOC + 66^\circ \\
   \Rightarrow \angle AOC = 120^\circ - 66^\circ \\
 $
$ \Rightarrow \angle AOC = 54^\circ $
So, we concluded that $\angle AOC = 54^\circ $ and $\angle BOC = 66^\circ $.
$ \Rightarrow $Option D is correct.

Note: This a basic question based on the properties of the triangle, which is that angles opposite to equal sides are equal. So, here we just need to remember the properties of the isosceles triangle other than that there is nothing much needed for solving this question.