
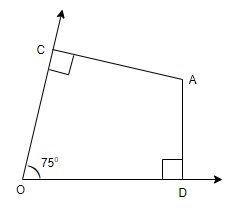
In the adjoining figure, $AC\bot OC$ and $AD\bot OD$. Find c.

Answer
597.3k+ views
Hint: From the figure given in the question, we can see that ACOD is a quadrilateral and we know that the sum of all angles of a quadrilateral is 360˚. Thus, $\angle ODA+\angle ACO+\angle COD+\angle CAD={{360}^{\circ }}$
From this relation, we will find $\angle CAD$.
Complete step-by-step solution -
It is given in the question that $AC\bot OC$ and $AD\bot OD$. Also, from the figure given in the question, we can see that $\angle COD={{75}^{\circ }}$. Then, we have to find the value of $\angle CAD$.
If we observe the figure given above, we can understand that it is a quadrilateral. We know the property of a quadrilateral that the sum of all the angles of a quadrilateral is 360˚. So, on applying this in our question, from the quadrilateral given, we can write that, $\angle ODA+\angle ACO+\angle COD+\angle CAD={{360}^{\circ }}.........(i)$
From the figure we can see that,
\[\begin{align}
& \angle COD={{75}^{\circ }} \\
& \angle ACO={{90}^{\circ }} \\
& \angle ODA={{90}^{\circ }} \\
\end{align}\]
So, on substituting all the above values in equation (i) we will get,
\[\begin{align}
& \Rightarrow {{90}^{\circ }}+{{90}^{\circ }}+{{75}^{\circ }}+\angle CAD={{360}^{\circ }} \\
& \Rightarrow \angle CAD+{{255}^{\circ }}={{360}^{\circ }} \\
& \Rightarrow \angle CAD={{360}^{\circ }}-{{255}^{\circ }} \\
& \Rightarrow \angle CAD={{105}^{\circ }} \\
\end{align}\]
Therefore, we get \[\angle CAD={{105}^{\circ }}\]. Hence the value of $\angle CAD$ is ${{105}^{\circ }}$.
Note: In this question, the possible mistake that the students can make is by thinking that $\angle CAD$ is an intersection point of two perpendicular lines and so will take the value of $\angle CAD$ as ${{90}^{\circ }}$, which is actually wrong. $\angle CAD$ is actually equal to ${{105}^{\circ }}$. Also the students must keep in mind that in this question, a quadrilateral is given and hence the sum of all the angles of a quadrilateral is 360˚. Some students may take the sum of all the angles as 180˚ but that is wrong. So, the students must be careful while solving the question.
From this relation, we will find $\angle CAD$.
Complete step-by-step solution -
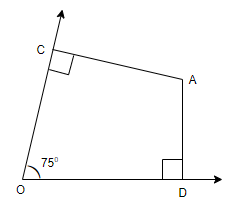
It is given in the question that $AC\bot OC$ and $AD\bot OD$. Also, from the figure given in the question, we can see that $\angle COD={{75}^{\circ }}$. Then, we have to find the value of $\angle CAD$.

If we observe the figure given above, we can understand that it is a quadrilateral. We know the property of a quadrilateral that the sum of all the angles of a quadrilateral is 360˚. So, on applying this in our question, from the quadrilateral given, we can write that, $\angle ODA+\angle ACO+\angle COD+\angle CAD={{360}^{\circ }}.........(i)$
From the figure we can see that,
\[\begin{align}
& \angle COD={{75}^{\circ }} \\
& \angle ACO={{90}^{\circ }} \\
& \angle ODA={{90}^{\circ }} \\
\end{align}\]
So, on substituting all the above values in equation (i) we will get,
\[\begin{align}
& \Rightarrow {{90}^{\circ }}+{{90}^{\circ }}+{{75}^{\circ }}+\angle CAD={{360}^{\circ }} \\
& \Rightarrow \angle CAD+{{255}^{\circ }}={{360}^{\circ }} \\
& \Rightarrow \angle CAD={{360}^{\circ }}-{{255}^{\circ }} \\
& \Rightarrow \angle CAD={{105}^{\circ }} \\
\end{align}\]
Therefore, we get \[\angle CAD={{105}^{\circ }}\]. Hence the value of $\angle CAD$ is ${{105}^{\circ }}$.
Note: In this question, the possible mistake that the students can make is by thinking that $\angle CAD$ is an intersection point of two perpendicular lines and so will take the value of $\angle CAD$ as ${{90}^{\circ }}$, which is actually wrong. $\angle CAD$ is actually equal to ${{105}^{\circ }}$. Also the students must keep in mind that in this question, a quadrilateral is given and hence the sum of all the angles of a quadrilateral is 360˚. Some students may take the sum of all the angles as 180˚ but that is wrong. So, the students must be careful while solving the question.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




