Question

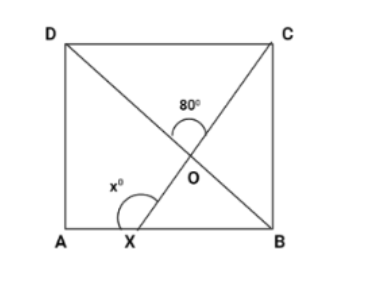
In the adjoining figure, $ABCD$ is a square. A line segment $CX$ cuts $AB$ at $X$ and the diagonal $BD$ at $O$ such that $\angle COD = {80^o}$ and $\angle OXA = {x^o}$. Find the value of $x$.

Answer 1

Hint: We will use exterior angle sum property for the above question. The sum of the two opposing interior angles equals a triangle's exterior angle. ${180^o}$ is the sum of the outer and internal angles. Also, when two lines converge, two pairs of opposite angles are formed. opposite angles are often congruent, which means they are identical.

Complete step by step solution:
We know that when two lines intersect, then the opposite angles are equal. In the figure, $\angle DOC = \angle XOB$
It is given in the question that $\angle DOC = {80^o}$
Hence, $\angle XOB = {80^o} - (i)$
We also know that the diagonal divides the angles of the squares into two equal parts.
Since, $\angle ABC = {90^o}$, then $\angle DBA = {45^o} - (ii)$
Now, when we apply exterior angle sum property to the $\Delta XOB$, we get,
$
  \angle AXO = \angle XOB + \angle XBA \\
  \angle AXO = \angle XOB + \angle DBA \;
 $
Substituting the values from $(i)$ and $(ii)$
$
  \angle AXO = \angle XOB + \angle DBA \\
  \angle AXO = {80^o} + {45^o} \\
  \angle AXO = {125^o} \;
 $
Hence, the final answer is $x = {125^o}$.
So, the correct answer is “ $x = {125^o}$”.

Note: We can also use the angle sum property of a triangle in place of exterior angle sum property. The Triangle Angle Sum Theorem states that the sum of a triangle's three inner angles is always ${180^o}$. We can calculate the value of x, by subtracting $180$with $\angle OXB$.